题目内容
已知a2-a+1=0,求a2010+
的值.
| 1 |
| a2010 |
考点:完全平方公式
专题:计算题
分析:由已知等式变形得到a2=a-1,a2-a=-1,依次求出a3,a4,a5,a6,a7,进而得到a6=1,原式变形后计算即可得到结果.
解答:解:由a2-a+1=0,得到a2=a-1,a2-a=-1,
∴a3=a2•a=a(a-1)=a2-a=-1;
a4=a3•a=-a;
a5=a4•a=-a2=1-a;
a6=a5•a=a(1-a)=a-a2=1;
a7=a6•a=a,即a6=1,
∵2010÷6=335,
∴a2010=(a6)335=1,
则a2010+
=1+1=2.
∴a3=a2•a=a(a-1)=a2-a=-1;
a4=a3•a=-a;
a5=a4•a=-a2=1-a;
a6=a5•a=a(1-a)=a-a2=1;
a7=a6•a=a,即a6=1,
∵2010÷6=335,
∴a2010=(a6)335=1,
则a2010+
| 1 |
| a2010 |
点评:此题考查了完全平方公式,熟练掌握公式是解本题的关键.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
 如图,AB为圆O的直径,点C是圆O上一点,AC平分∠DAB,AD⊥CD,线段AB与DC的延长线交于点P.
如图,AB为圆O的直径,点C是圆O上一点,AC平分∠DAB,AD⊥CD,线段AB与DC的延长线交于点P. 如图在△ABC中,∠B=30°,AD⊥AB,垂足为A,AD=1cm,求AB的长.
如图在△ABC中,∠B=30°,AD⊥AB,垂足为A,AD=1cm,求AB的长.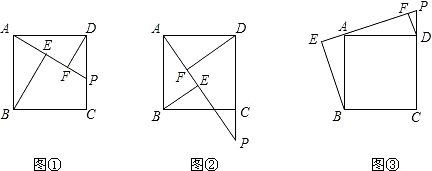
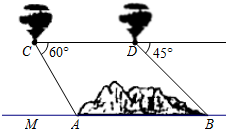 如图,我省在修建泛亚铁路时遇到一座山,要从A地向B地修一条隧道(A,B在同一水平面上),为了测量A,B两地之间的距离,某工程师乘坐热气球从M地出发垂直上升150 米到达C处,在C处观察A地的俯角为60°,然后保持同一高度向前平移200米到达D处,在D处观察B地的俯角为45°,则A、B两地之间的距离为多少米?(参考数据:
如图,我省在修建泛亚铁路时遇到一座山,要从A地向B地修一条隧道(A,B在同一水平面上),为了测量A,B两地之间的距离,某工程师乘坐热气球从M地出发垂直上升150 米到达C处,在C处观察A地的俯角为60°,然后保持同一高度向前平移200米到达D处,在D处观察B地的俯角为45°,则A、B两地之间的距离为多少米?(参考数据: