题目内容
2.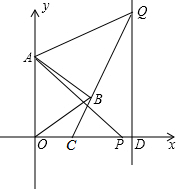 如图,已知等边△AOB的顶点O与原点重合,点A的坐标为(0,2$\sqrt{3}$),点P(t,0)为x轴上一动点(不与O重合).连结AP,将AP绕点A逆时针旋转60°得到线段AQ,连结QB并延长交x轴于点C.过Q作x轴的垂线,垂足为D.
如图,已知等边△AOB的顶点O与原点重合,点A的坐标为(0,2$\sqrt{3}$),点P(t,0)为x轴上一动点(不与O重合).连结AP,将AP绕点A逆时针旋转60°得到线段AQ,连结QB并延长交x轴于点C.过Q作x轴的垂线,垂足为D.(1)直接写出点B的坐标,并求当t=4时,BQ的长度.
(2)当t>0时,求△QCP的面积S与t的函数关系式.
(3)在直线QD上存在点M,使△BPM成为等腰直角三角形,请直接写出所有符合条件的t的值.
分析 (1)证明△AOP≌△ABQ,即可得到BQ=OP=4;
(2)由△AOP≌△ABQ,得到△OCB是等腰三角形,进而表示出OC、CP、CQ、QD的长度,求△QCP的面积S与t的函数关系式;
(3)存在,分三种情况分类讨论,列方程组求解即可.
解答 解:(1)由题意知,△AOB和△AQP都是等边三角形,
∴AO=AB,AP=AQ,∠OAP=60°-∠PAB=∠BAQ,
∴△AOP≌△ABQ,
∴BQ=OP=4;
(2)∵△AOP≌△ABQ,
∴∠ABQ=90°,∠OBC=30°,
∵∠BOC=30°,
∴∠BCP=60°,
在等腰三角形OCB中,OB=2$\sqrt{3}$,
∴OC=BC=2,CQ=t+2,CP=t-2,
∴S△CPQ=$\frac{1}{2}$•(t+2)•(t-2)•sin60°=$\frac{\sqrt{3}}{4}$(t2-4),
∴①当0<t<2时,S=$\frac{\sqrt{3}}{4}$(t2-4),
②当t>2时,S=$\frac{\sqrt{3}}{4}$(t2-4);
(3)存在,t=$6+2\sqrt{3}$或$6-2\sqrt{3}$或$2\sqrt{3}$或$-2\sqrt{3}$,
在直线QD上存在点M,使△BPM成为等腰直角三角形,有三种可能:
①BP2+PM2=BM2且BP=PM
②BP2+BM2=PM2且BP=BM
③BM2+PM2=BP2且BM=PM
分别列方程组解得:t=$6+2\sqrt{3}$或$6-2\sqrt{3}$或$2\sqrt{3}$或$-2\sqrt{3}$.
点评 本题考查了运用数形结合的方法解决几何变换问题,主要考查了三角形全等的性质和判定,等腰三角形的性质和判定,勾股定理,三角函数以及列方程(组)等知识的综合运用.

练习册系列答案
相关题目
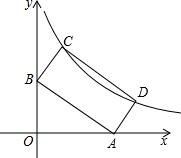 如图点P($\sqrt{5}$+1,$\sqrt{5}$-1)在双曲线y=$\frac{k}{x}$(x>0)上.
如图点P($\sqrt{5}$+1,$\sqrt{5}$-1)在双曲线y=$\frac{k}{x}$(x>0)上.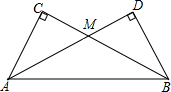 把两个同样大小的含30°角的三角尺像如图所示那样放置,其中M是AD与BC的交点,这时MC的长度就等于点M到AB的距离.你知道这是为什么吗?
把两个同样大小的含30°角的三角尺像如图所示那样放置,其中M是AD与BC的交点,这时MC的长度就等于点M到AB的距离.你知道这是为什么吗?

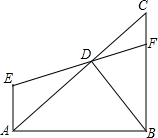 如图,∠ABC=90°,AE∥BC,D为AC上的一点,连接ED并延长交BC于点F,且∠ABD=∠DAE,问:BD与AC的位置关系如何?说明理由.
如图,∠ABC=90°,AE∥BC,D为AC上的一点,连接ED并延长交BC于点F,且∠ABD=∠DAE,问:BD与AC的位置关系如何?说明理由.