题目内容
19.已知任意三角形的内角和为180°,试利用多边形中过某一顶点的对角线的条数,探求多边形内角和公式.(1)如图所示,一个四边形可以分成2个三角形;于是四边形的内角和为360°;
(2)一个五边形可以分成3个三角形;于是五边形的内角和为540°;
(3)按此规律,n(n≥3)边形可分成多少个三角形?n边形的内角和是多少度?

分析 (1)根据四边形可分为两个三角形可得出结论;
(3)根据五边形可分为三个三角形可得出结;
(2)观察每组因数之间的关系,在观察相应结果有什么关系,就可以得出结论.
解答 解:(1)∵四边形可分为两个三角形,
∴四边形的内角和=180°×2=360°.
故答案为:2,360°;
(2))∵五边形可分为三个三角形,
∴四边形的内角和=180°×3=540°.
故答案为:3,540°;
(3)由(1)、(2)可知,过n边形一个顶点的对角线将n边形可以分成(n-2)个三角形,于是n边形的内角和为(n-2)•180°.
故答案为:n-2,(n-2)•180°.
点评 本题考查的是多边形的内角和,熟知观察出过n边形一个顶点的对角线将n边形可以分成的三角形的个数比边数少2是解题的关键.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
8. 如图,AB∥CD,DB⊥BC,∠1=30°,则∠2的度数是( )
如图,AB∥CD,DB⊥BC,∠1=30°,则∠2的度数是( )
 如图,AB∥CD,DB⊥BC,∠1=30°,则∠2的度数是( )
如图,AB∥CD,DB⊥BC,∠1=30°,则∠2的度数是( )| A. | 40° | B. | 50° | C. | 60° | D. | 140° |


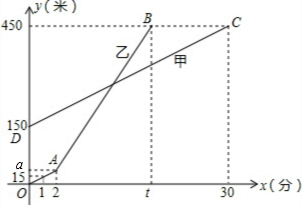 甲乙两人同时登山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,请根据图象提供的信息解答下列问题:
甲乙两人同时登山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,请根据图象提供的信息解答下列问题: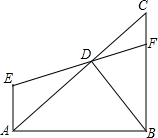 如图,∠ABC=90°,AE∥BC,D为AC上的一点,连接ED并延长交BC于点F,且∠ABD=∠DAE,问:BD与AC的位置关系如何?说明理由.
如图,∠ABC=90°,AE∥BC,D为AC上的一点,连接ED并延长交BC于点F,且∠ABD=∠DAE,问:BD与AC的位置关系如何?说明理由. 如图,三角形ABC中,BC=7cm,若三角形ABC沿射线BC方向向右平移2cm得到三角形A′B′C′,则CC′=2cm.
如图,三角形ABC中,BC=7cm,若三角形ABC沿射线BC方向向右平移2cm得到三角形A′B′C′,则CC′=2cm.