题目内容
20.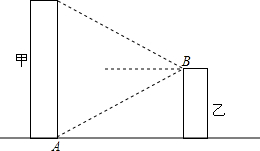 某城市搞亮化工程,如图,在甲楼底部,乙楼顶部分别安装一盏射灯.已知A灯恰好照到B灯,B灯恰好照到甲楼的顶部,如果两盏灯的光线与水平线的夹角相等,那么能否说甲楼的高度是乙楼的2倍?说说你的看法.
某城市搞亮化工程,如图,在甲楼底部,乙楼顶部分别安装一盏射灯.已知A灯恰好照到B灯,B灯恰好照到甲楼的顶部,如果两盏灯的光线与水平线的夹角相等,那么能否说甲楼的高度是乙楼的2倍?说说你的看法.
分析 首先过B作BF⊥AC,然后证明△CBF≌△ABF可得CF=AF,再证明四边形BFAE是矩形可得AF=BE,从而可得结论.
解答 解:能.
过B作BF⊥AC,
∵BF⊥AC,
∴∠CFB=∠BFA=90°,
∵两盏灯的光线与水平线的夹角相等,
∴∠CBF=∠ABF,
在△CBF和△ABF中,
$\left\{\begin{array}{l}{∠CBF=∠ABF}\\{BF=BF}\\{∠BFA=∠BFC}\end{array}\right.$,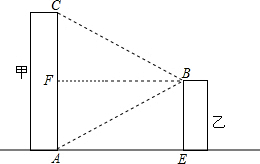
∴△CBF≌△ABF(ASA),
∴CF=AF,
∴AC=2AF,
∵∠BFA=90°,楼房垂直于地面,
∴四边形BFAE是矩形,
∴AF=BE,
∴AC=2BE,
∴甲楼的高度是乙楼的2倍.
点评 此题主要考查了全等三角形的应用,关键是正确掌握判定两个三角形全等的判定方法.

练习册系列答案
相关题目
8. 如图,直线a∥b,直线a⊥c,若∠1=70°,则∠2=( )
如图,直线a∥b,直线a⊥c,若∠1=70°,则∠2=( )
 如图,直线a∥b,直线a⊥c,若∠1=70°,则∠2=( )
如图,直线a∥b,直线a⊥c,若∠1=70°,则∠2=( )| A. | 70° | B. | 90° | C. | 20° | D. | 80° |
 如图,AB半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于D,连接BE.设∠BEC=α,则tanα的值为$\frac{3}{2}$.
如图,AB半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于D,连接BE.设∠BEC=α,则tanα的值为$\frac{3}{2}$.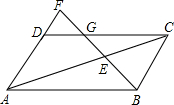 如图,?ABCD的边AD的延长线上取一点F,BF分别交AC,DC于点E,G,且EF=32cm,GF=18cm,求BE的长.
如图,?ABCD的边AD的延长线上取一点F,BF分别交AC,DC于点E,G,且EF=32cm,GF=18cm,求BE的长.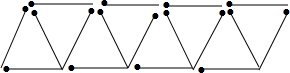 如图所示,用火柴棍拼成一排由三角形组成的图形.
如图所示,用火柴棍拼成一排由三角形组成的图形.