题目内容
5.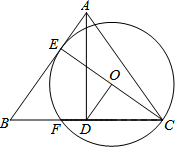 如图,在△ABC中,AB=AC,AD⊥BC于点D,过点C作⊙O与边AB相切于点E,交BC于点F,CE为⊙O的直径.
如图,在△ABC中,AB=AC,AD⊥BC于点D,过点C作⊙O与边AB相切于点E,交BC于点F,CE为⊙O的直径.(1)求证:OD⊥CE;
(2)若DF=1,DC=3,求AE的长.
分析 (1)⊙O与边AB相切于点E,且 CE为⊙O的直径,得到CE⊥AB,由等腰三角形的性质三线合一得到BD=DC,根据三角形的中位线的性质得到结论;
(2)连接EF,由CE为⊙O的直径,且点F在⊙O上,得到∠EFC=90°,又因为 CE⊥AB,得到∠BEF+∠FEC=∠FEC+∠ECF=90°,推出∠BEF=∠ECF,于是得到tan∠BEF=tan∠ECF,得到等积式$\frac{BF}{EF}=\frac{EF}{FC}$,求得EF=2$\sqrt{2}$,由勾股定理得BE,再根据平行线分线段成比例,列出比例式求解.
解答 解:(1)∵⊙O与边AB相切于点E,且 CE为⊙O的直径,
∴CE⊥AB,
∵AB=AC,AD⊥BC,
∴BD=DC,
又∵OE=OC,
∴OD∥EB,
∴OD⊥CE;
(2)连接EF,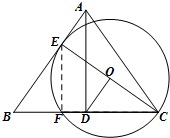 ∵CE为⊙O的直径,且点F在⊙O上,∴∠EFC=90°,
∵CE为⊙O的直径,且点F在⊙O上,∴∠EFC=90°,
∵CE⊥AB,
∴∠BEC=90°.
∴∠BEF+∠FEC=∠FEC+∠ECF=90°,
∴∠BEF=∠ECF,
∴tan∠BEF=tan∠ECF
∴$\frac{BF}{EF}=\frac{EF}{FC}$,
又∵DF=1,BD=DC=3,
∴BF=2,FC=4,
∴EF=2$\sqrt{2}$,
∵∠EFC=90°,
∴∠BFE=90°,
由勾股定理,得$BE=\sqrt{B{F^2}+E{F^2}}=2\sqrt{3}$,
∵EF∥AD,
∴$\frac{BE}{EA}=\frac{BF}{FD}=\frac{2}{1}$,
∴$AE=\sqrt{3}$.
点评 本题考查了切线的性质,圆周角定理,锐角三角形函数,勾股定理,平行线的性质,正确的作出辅助线是解题的关键.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
14.下列计算正确的是( )
| A. | a+2a=3a2 | B. | (ab2)3=a3b6 | C. | (am)2=am+2 | D. | a3•a2=a6 |
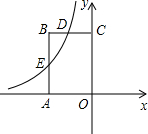 如图,矩形OABC的顶点A,C分别在x轴和y轴上,若OA=4,OC=6,写出一个函数y=$\frac{k}{x}({k≠0})$,使它的图象与矩形OABC的两边AB,BC分别交于点D,E,这个函数的表达式为y=-$\frac{1}{x}$.
如图,矩形OABC的顶点A,C分别在x轴和y轴上,若OA=4,OC=6,写出一个函数y=$\frac{k}{x}({k≠0})$,使它的图象与矩形OABC的两边AB,BC分别交于点D,E,这个函数的表达式为y=-$\frac{1}{x}$.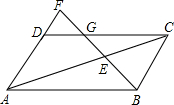 如图,?ABCD的边AD的延长线上取一点F,BF分别交AC,DC于点E,G,且EF=32cm,GF=18cm,求BE的长.
如图,?ABCD的边AD的延长线上取一点F,BF分别交AC,DC于点E,G,且EF=32cm,GF=18cm,求BE的长.