题目内容
8．若关于x的一元二次方程ax2+4x-2=0有两个实数根，则a的取值范围是a≥-2且a≠0．分析 由关于x的一元二次方程ax2+4x-2=0有有两个实数根及一元二次方程的定义，即可得判别式△≥0，a≠0，继而可求得a的范围．
解答 解：∵关于x的一元二次方程ax2+4x-2=0有两个实数根，
∴△=b2-4ac=42-4×a×（-2）=4-24a≥0，
解得：a≥-2，
∵方程ax2-2x+6=0是一元二次方程，
∴a≠0，
∴a的范围是：a≥-2且a≠0，
故答案为：a≥-2且a≠0．
点评 此题考查了一元二次方程判别式的知识．此题比较简单，注意掌握一元二次方程有两个实数根，即可得△≥0．同时考查了一元二次方程的定义．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
16．
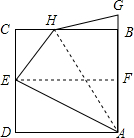将正方形纸片ABCD按如图所示对折，使边AD与BC重合，折痕为EF，连接AE，将AE折叠到AB上，折痕为AH，则$\frac{BH}{BC}$的值是$\frac{\sqrt{5}-1}{2}$．
将正方形纸片ABCD按如图所示对折，使边AD与BC重合，折痕为EF，连接AE，将AE折叠到AB上，折痕为AH，则$\frac{BH}{BC}$的值是$\frac{\sqrt{5}-1}{2}$． 
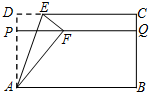如图，在矩形纸片ABCD中，AD=12cm，现将这张纸片按下列图示方式折叠，AE是折痕．若DP=$\frac{1}{n}$AD，CQ=$\frac{1}{n}$BC，点D的对应点F在PQ上，则AE的长是12$\sqrt{\frac{2n}{2n-1}}$cm．
20．一组数据2，3，5，4，4，6的中位数和平均数分别是（ ）
| A． | 4.5和4 | B． | 4和4 | C． | 4和4.8 | D． | 5和4 |
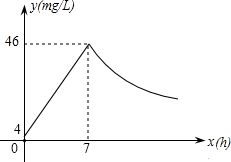近年来，我国煤矿安全事故频频发生，其中危害最大的是瓦斯，其主要成分是CO，在一次矿难事件的调查中发现：从零时起，井内空气中CO的浓度达到4mg/L，此后浓度呈直线型增加，在第7小时达到最高值46mg/L，发生爆炸；爆炸后，空气中的CO浓度成反比例下降，如图所示，根据题中相关信息回答下列问题：