题目内容
1.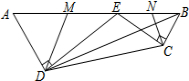 如图,在四边形ABCD中,E为AB边上一点,ED⊥AD于D,EC⊥CB于C,且∠AED=∠BEC,AB=2$\sqrt{13}$,AD=3,BD=$\sqrt{37}$,M、N分别为AE、BE的中点,连接DM、CN,则△DEM与△CEN的周长之和为2$\sqrt{13}$+6.
如图,在四边形ABCD中,E为AB边上一点,ED⊥AD于D,EC⊥CB于C,且∠AED=∠BEC,AB=2$\sqrt{13}$,AD=3,BD=$\sqrt{37}$,M、N分别为AE、BE的中点,连接DM、CN,则△DEM与△CEN的周长之和为2$\sqrt{13}$+6.
分析 根据三角形相似,从而得到∠A=∠ABC,进而补全等腰三角形,△DEM与△CEN的周长之和就可转化为AB+BH,而BH是△ADB的边AD上的高,只需利用勾股定理建立方程,求出DH,再求出BH,就可解决问题.
解答 解:延长AD、BC交于点F,作BH⊥AF,垂足为H,如图,
∵ED⊥AD,EC⊥CB,
∴∠ADE=∠BCE=90°,
又∵∠AED=∠BEC,
∴△ADE∽△BCE,
∴∠A=∠CBE,
∴FA=FB.
连接EF,∵S△ABF=S△AEF+S△BEF,
即$\frac{1}{2}$AF•BH=$\frac{1}{2}$AF•DE+$\frac{1}{2}$BF•CE,
∴ED+EC=BH,
设DH=x,则AH=AD+DH=(3+x).
∵BH⊥AF,
∴∠BHA=90°.
∴BH2=BD2-DH2=AB2-AH2.
∵AB=2$\sqrt{13}$,AD=3,BD=$\sqrt{37}$,
∴($\sqrt{37}$)2-x2=(2$\sqrt{13}$)2-(3+x)2,
解得:x=1.
∴BH2=BD2-DH2=37-1=36,
∴BH=6,
∴ED+EC=BH=6,
∵∠ADE=∠BCE=90°,
且M、N分别为AE、BE的中点,
∴DM=AM=EM=$\frac{1}{2}$AE,CN=BN=EN=$\frac{1}{2}$BE.
∴△DEM与△CEN的周长之和
=DE+DM+EM+CN+EN+EC
=DE+AE+BE+EC=DE+AB+EC
=DE+EC+AB=2$\sqrt{13}$+6.
即△DEM与△CEN的周长之和为2$\sqrt{13}$+6.
故答案为:2$\sqrt{13}$+6.
点评 本题考查了相似三角形的性质与判定,三角形的面积的计算,平行线的性质与判定、直角三角形斜边上的中线等于斜边的一半、勾股定理等知识,考查了用面积法证明几何问题,考查了运用已有的经验解决问题的能力,体现了自主探究与合作交流的新理念,是充分体现新课程理念难得的好题.

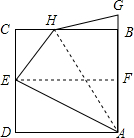 将正方形纸片ABCD按如图所示对折,使边AD与BC重合,折痕为EF,连接AE,将AE折叠到AB上,折痕为AH,则$\frac{BH}{BC}$的值是$\frac{\sqrt{5}-1}{2}$.
将正方形纸片ABCD按如图所示对折,使边AD与BC重合,折痕为EF,连接AE,将AE折叠到AB上,折痕为AH,则$\frac{BH}{BC}$的值是$\frac{\sqrt{5}-1}{2}$. 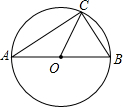 如图,AB是⊙O的直径,BC是⊙O的弦.若∠OBC=60°,则∠BAC的度数是( )
如图,AB是⊙O的直径,BC是⊙O的弦.若∠OBC=60°,则∠BAC的度数是( )| A. | 75° | B. | 60° | C. | 45° | D. | 30° |
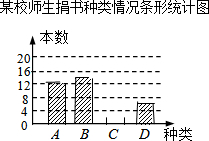 在读书月活动中,某校号召全体师生积极捐书,为了解所捐书籍的种类,图书管理员对部分书籍进行了抽样调查,根据调查数据绘制了如下不完整的统计图表.请你根据统计图表所提供的信息回答下面问题:
在读书月活动中,某校号召全体师生积极捐书,为了解所捐书籍的种类,图书管理员对部分书籍进行了抽样调查,根据调查数据绘制了如下不完整的统计图表.请你根据统计图表所提供的信息回答下面问题:某校师生捐书种类情况统计表
| 种类 | 频数 | 百分比 |
| A.科普类 | 12 | n |
| B.文学类 | 14 | 35% |
| C.艺术类 | m | 20% |
| D.其它类 | 6 | 15% |
(2)补全条形统计图;
(3)本次活动师生共捐书2000本,请估计有多少本科普类图书?
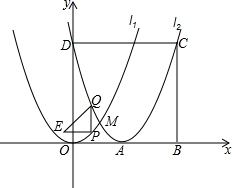 如图,以A为顶点的抛物线l2是由抛物线l1:y=x2沿x轴向右平移2个单位后得到的,两抛物线相交于点M,抛物线l2与y轴交于点D,以OD为边向右作正方形ODCB,P为抛物线l1上一点,其横坐标为m(0≤m≤2),且点P不与点M重合,过点P作PQ∥y轴,交抛物线l2于点Q,将PQ绕点P逆时针旋转90°,得到线段PE,连结EQ.
如图,以A为顶点的抛物线l2是由抛物线l1:y=x2沿x轴向右平移2个单位后得到的,两抛物线相交于点M,抛物线l2与y轴交于点D,以OD为边向右作正方形ODCB,P为抛物线l1上一点,其横坐标为m(0≤m≤2),且点P不与点M重合,过点P作PQ∥y轴,交抛物线l2于点Q,将PQ绕点P逆时针旋转90°,得到线段PE,连结EQ.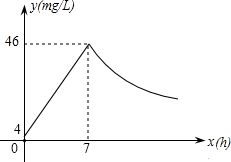 近年来,我国煤矿安全事故频频发生,其中危害最大的是瓦斯,其主要成分是CO,在一次矿难事件的调查中发现:从零时起,井内空气中CO的浓度达到4mg/L,此后浓度呈直线型增加,在第7小时达到最高值46mg/L,发生爆炸;爆炸后,空气中的CO浓度成反比例下降,如图所示,根据题中相关信息回答下列问题:
近年来,我国煤矿安全事故频频发生,其中危害最大的是瓦斯,其主要成分是CO,在一次矿难事件的调查中发现:从零时起,井内空气中CO的浓度达到4mg/L,此后浓度呈直线型增加,在第7小时达到最高值46mg/L,发生爆炸;爆炸后,空气中的CO浓度成反比例下降,如图所示,根据题中相关信息回答下列问题: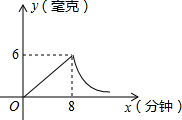 为了预防流行性感冒,某学校对教室采用药熏消毒法进行消毒.已知药物燃烧时室内每立方米空气中的含药量y毫克)与时间x(分钟)成正比例;药物燃烧后,y与x成反比例(如图所示).请根据图中提供的信息,解答下列问题:
为了预防流行性感冒,某学校对教室采用药熏消毒法进行消毒.已知药物燃烧时室内每立方米空气中的含药量y毫克)与时间x(分钟)成正比例;药物燃烧后,y与x成反比例(如图所示).请根据图中提供的信息,解答下列问题: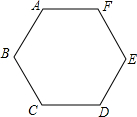 如图,已知点A、B、C、D、E、F是边长为1的正六边形的顶点,连接任意两点均可得到一条线段,在连接两点所得的所有线段中任取一条线段,取得长度为$\sqrt{3}$的线段的概率为$\frac{2}{5}$.
如图,已知点A、B、C、D、E、F是边长为1的正六边形的顶点,连接任意两点均可得到一条线段,在连接两点所得的所有线段中任取一条线段,取得长度为$\sqrt{3}$的线段的概率为$\frac{2}{5}$.