题目内容
2.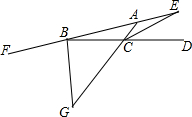 如图所示,在△ABC中,点D是BC延长线上的点,点F是AB延长线上的点.∠ACD的平分线交BA延长线于点E,∠FBC的平分线交AC延长线于点G.若CE=BC=BG,则∠ABC的度数12度.
如图所示,在△ABC中,点D是BC延长线上的点,点F是AB延长线上的点.∠ACD的平分线交BA延长线于点E,∠FBC的平分线交AC延长线于点G.若CE=BC=BG,则∠ABC的度数12度.
分析 可设∠ABC的度数是x度,根据三角形外角的性质和等腰三角形的性质得到∠DCE=2x度,根据角平分线的性质得到∠DCA=4x度,根据三角形外角的性质和等腰三角形的性质和对顶角相等得到∠BCG=4x度,∠G=4x度,∠BAC=3x度,∠FBG=7x度,根据角平分线的性质得到∠DBG=7x度,再根据平角的定义即可求解.
解答 解:设∠ABC的度数是x度,
∵CE=BC,
∴∠DCE=2x度,
∵∠ACD的平分线交BA延长线于点E,
∴∠DCA=4x度,
∴∠BCG=4x度,
∵BC=BG,
∴∠G=4x度,
∴∠BAC=3x度,
∴∠FBG=7x度,
∵∠FBC的平分线交AC延长线于点G,
∴∠DBG=7x度,
∴7x+7x+x=180,
解得x=12.
故答案为:12.
点评 此题主要考查了角平分线的性质,三角形内角与外角的关系,关键是熟练掌握三角形外角的性质;三角形的一个外角等于和它不相邻的两个内角的和.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
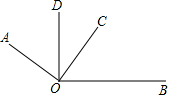 如图,∠AOC与∠BOD都是直角.
如图,∠AOC与∠BOD都是直角.