题目内容
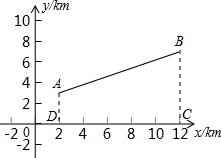 去冬今春,济宁市遭遇了200年不遇的大旱,某乡镇为了解决抗旱问题,要在某河道建一座水泵站,分别向河的同一侧张村A和李村B送水.经实地勘查后,工程人员设计图纸时,以河道上的大桥O为坐标原点,以河道所在的直线为x轴建立直角坐标系(如图).两村的坐标分别为A(2,3),B(12,7).
去冬今春,济宁市遭遇了200年不遇的大旱,某乡镇为了解决抗旱问题,要在某河道建一座水泵站,分别向河的同一侧张村A和李村B送水.经实地勘查后,工程人员设计图纸时,以河道上的大桥O为坐标原点,以河道所在的直线为x轴建立直角坐标系(如图).两村的坐标分别为A(2,3),B(12,7).(1)若从节约经费考虑,水泵站建在距离大桥多远的地方可使所用输水管道最短?
(2)若水泵达到张村,李村的距离相等,请你直接在图上画出水泵站的具体位置P(不写作法,保留作图痕迹).
考点:轴对称-最短路线问题,坐标与图形性质
专题:
分析:(1)为了使所修水泵站的所用输水管道最短,利用轴对称的方法画图可求;
(2)所求点要满足两个条件,到张村和李村的距离相等,可以作连接两村线段的垂直平分线,与x轴的交点即为所求.
(2)所求点要满足两个条件,到张村和李村的距离相等,可以作连接两村线段的垂直平分线,与x轴的交点即为所求.
解答: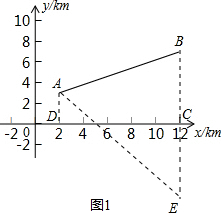 解:(1)如图1,作点B关于x轴的对称点E,连接AE,则点E为(12,-7)
解:(1)如图1,作点B关于x轴的对称点E,连接AE,则点E为(12,-7)
设直线AE的函数关系式为y=kx+b(k≠0),则
,
解得
,
当y=0时,x=5.
所以,水泵站建在距离大桥5千米的地方,可使所用输水管道最短.
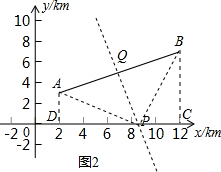
(2)如图2所示,作线段AB的垂直平分线PQ,交x轴于点P,P即为所求;
 解:(1)如图1,作点B关于x轴的对称点E,连接AE,则点E为(12,-7)
解:(1)如图1,作点B关于x轴的对称点E,连接AE,则点E为(12,-7)设直线AE的函数关系式为y=kx+b(k≠0),则
|
解得
|
当y=0时,x=5.
所以,水泵站建在距离大桥5千米的地方,可使所用输水管道最短.
(2)如图2所示,作线段AB的垂直平分线PQ,交x轴于点P,P即为所求;

点评:本题考查了待定系数法求一次函数解析式,线段的垂直平分线,轴对称的作图方法.关键是明确每条线上点的性质,合理地选择.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
 如图,已知∠AOB=30°,点P在∠AOB的内部,OP=6.
如图,已知∠AOB=30°,点P在∠AOB的内部,OP=6.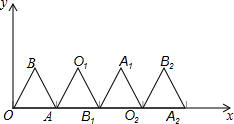 如图,在平面直角坐标系中有一个等边△OBA,其中A点坐标为(1,0).将△OBA绕顶点A顺时针旋转120°,得到△AO1B1;将得到的△AO1B1绕顶点B1顺时针旋转120°,得到△B1A1O2;然后再将得到的△B1A1O2绕顶点O2顺时针旋转120°,得到△O2B2A2…按照此规律,继续旋转下去,则A2014点的坐标为
如图,在平面直角坐标系中有一个等边△OBA,其中A点坐标为(1,0).将△OBA绕顶点A顺时针旋转120°,得到△AO1B1;将得到的△AO1B1绕顶点B1顺时针旋转120°,得到△B1A1O2;然后再将得到的△B1A1O2绕顶点O2顺时针旋转120°,得到△O2B2A2…按照此规律,继续旋转下去,则A2014点的坐标为 (1)请找出该残片所在圆的圆心位置,其中点A、B、C在圆上(保留画图痕迹,不必写画法);
(1)请找出该残片所在圆的圆心位置,其中点A、B、C在圆上(保留画图痕迹,不必写画法);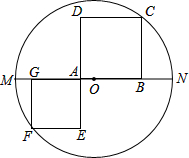 如图,MN是⊙O的直径,MN=6,B是线段ON上一动点,四边形ABCD和AEFG都是正方形,其中点G,A在MN上,点C,F在图上,则正方形ABCD与正方形AEFG的面积和为
如图,MN是⊙O的直径,MN=6,B是线段ON上一动点,四边形ABCD和AEFG都是正方形,其中点G,A在MN上,点C,F在图上,则正方形ABCD与正方形AEFG的面积和为