题目内容
2.下边横排有15个方格,每个方格中都只有一个数字,且任何相邻三个数字之和都是16.| 6 | m | n |
(2)利用你在解决(1)时发现的规律,设计一个在本题背景下相关的拓展问题,或给出设计思路(可以增加条件,不用解答).
你所设计的问题(或设计思路)是:
分析 根据任何相邻的三个数字之和都是16可以求出第二个与第三个空格的数字之和是10,所以第四个空格的数字是6,依此类推,第7个空格的数字是6,第10个空格数字是6,第13个空格的数字是6,得到答案.
解答 解:(1)根据题意,设第二空格、第三空格数为a、b,
依题意,得a+b=16-6=10,
∴第四个空格是6,依此规律,数字是6的空格有第7个,第10个,第13个,
即m=6,n=6,
故答案为:6;6;
(2)一个五位数,相邻三个数字之和是16,个位上是7、十位上是3,这个五位数是多少?
点评 本题考查的是数字的变化类问题,正确找出数字的变化规律是解题的关键.

练习册系列答案
 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
13.在现实生活中,铺地最常见的是用正方形地板砖,某小区广场准备用多种地板砖组合铺设,则能够选择的组合是( )
| A. | 正三角形,正方形 | B. | 正方形,正六边形 | ||
| C. | 正五边形,正六边形 | D. | 正六边形,正八边形 |
10. 如图,点O为直线AB上一点,OC⊥OD,若∠1=35°,则∠2的度数是( )
如图,点O为直线AB上一点,OC⊥OD,若∠1=35°,则∠2的度数是( )
 如图,点O为直线AB上一点,OC⊥OD,若∠1=35°,则∠2的度数是( )
如图,点O为直线AB上一点,OC⊥OD,若∠1=35°,则∠2的度数是( )| A. | 35° | B. | 45° | C. | 55° | D. | 65° |
17.小丽同学准备用自己节省的零花钱购买一台学生平板电脑,她已存有750元,并计划从本月起每月节省30元,直到她至少存有1080元,设x个月后小丽至少有1080元,则可列计算月数的不等式为( )
| A. | 30x+750>1080 | B. | 30x-750≥1080 | C. | 30x-750≤1080 | D. | 30x+750≥1080 |
7. 如图,已知∠AOB=70°,OC平分∠AOB,DC∥OB,则∠C为( )
如图,已知∠AOB=70°,OC平分∠AOB,DC∥OB,则∠C为( )
 如图,已知∠AOB=70°,OC平分∠AOB,DC∥OB,则∠C为( )
如图,已知∠AOB=70°,OC平分∠AOB,DC∥OB,则∠C为( )| A. | 20° | B. | 35° | C. | 45° | D. | 70° |
6.某日王老师佩戴运动手环进行快走锻炼,两次锻炼后数据如表.与第一次锻炼相比,王老师第二次锻炼步数增长的百分率是其平均步长减少的百分率的3倍.设王老师第二次锻炼时平均步长减少的百分率为x(0<x<0.5).
注:步数×平均步长=距离.
(1)根据题意完成表格填空;
(2)求x;
(3)王老师发现好友中步数排名第一为24000步,因此在两次锻炼结束后又走了500米,使得总步数恰好为24000步,求王老师这500米的平均步长.
| 项目 | 第一次锻炼 | 第二次锻炼 |
| 步数(步) | 10000 | ①10000(1+3x) |
| 平均步长(米/步) | 0.6 | ②0.6(1-x) |
| 距离(米) | 6000 | 7020 |
(1)根据题意完成表格填空;
(2)求x;
(3)王老师发现好友中步数排名第一为24000步,因此在两次锻炼结束后又走了500米,使得总步数恰好为24000步,求王老师这500米的平均步长.
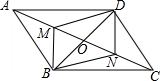 如图,在平行四边形ABCD中,M、N分别是OA,OC的中点,O为对角线AC与BD的交点,试问四边形BMDN是平行四边形吗?说说你的理由.
如图,在平行四边形ABCD中,M、N分别是OA,OC的中点,O为对角线AC与BD的交点,试问四边形BMDN是平行四边形吗?说说你的理由.