题目内容
11.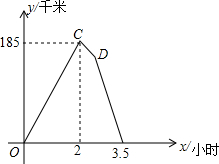 下面的图象反映的过程是:
下面的图象反映的过程是:甲、乙两人同时从A地出发,以各自的速度匀速向B地行驶,甲先到B地停留半小时后,按原路以另一速度匀速返回,直至与乙相遇.乙的速度为60千米/时,y(千米)表示甲、乙两人相距的距离,x(小时)表示乙行驶的时间.请根据图象回答下列问题:
(1)A、B两地相距多少千米?
(2)求点D的坐标.
(3)甲往返的速度分别是多少?
分析 (1)根据题意解方程得出甲车得速度,然后根据题意求得A、B两地的距离即可.
(2)根据两车之间的距离y(千米)与乙车行驶时间x(小时)之间的函数关系及乙车的速度为每小时60千米可得出D的坐标;
(3)根据题意列出方程,通过解方程得出甲车得速度.
解答 解:(1)设甲的速度为xkm/h,根据题意得
2(x-60)=185,
解得:x=152.5,
由于152.5×2=305,
故A、B两地相距305千米;
(2)∵甲车先到达B地,停留半小时后按原路以另一速度匀速返回,
∴D的横轴应为2.5;
∵乙车的速度为每小时60千米,
∴半小时后行驶距离为30km,故纵轴应为185-30=155;
∴点D的坐标(2.5,155).
(3)由(1)可知甲车去时的速度为152千米/时;
设甲车返回时行驶速度v千米/时,则
(v+60)×1=155,
解得v=95.
故甲返回的速度是95千米/时.
点评 本题主要考查了一次函数的综合题,解答要注意数形结合思想的运用,是各地中考的热点,同学们要加强训练,属于中档题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
3.化简:(a+$\frac{3a-4}{a-3}$)(1-$\frac{1}{a-2}$)的结果等于( )
| A. | a-2 | B. | a+2 | C. | $\frac{a-2}{a-3}$ | D. | $\frac{a-3}{a-2}$ |
20.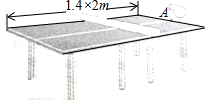 某乒乓球馆使用发球机进行辅助训练,出球口在桌面中线端点A处的正上方,假设每次发出的乒乓球的运动路线固定不变,且落在中线上.在乒乓球运行时,设乒乓球与端点A的水平距离为x(米),与桌面的高度为y(米),运行时间为t(秒),经多次测试后,得到如下部分数据:
某乒乓球馆使用发球机进行辅助训练,出球口在桌面中线端点A处的正上方,假设每次发出的乒乓球的运动路线固定不变,且落在中线上.在乒乓球运行时,设乒乓球与端点A的水平距离为x(米),与桌面的高度为y(米),运行时间为t(秒),经多次测试后,得到如下部分数据:
(1)当t为何值时,乒乓球达到最大高度?
(2)乒乓球落在桌面时,与端点A的水平距离是多少?
(3)乒乓球落在桌面上弹起后,y与x满足y=a(x-3)2+k.
①用含a的代数式表示k;
②球网高度为0.14米,球桌长(1.4×2)米.若球弹起后,恰好有唯一的击球点,可以将球沿直线恰好擦网扣杀到A,求a的值.
 某乒乓球馆使用发球机进行辅助训练,出球口在桌面中线端点A处的正上方,假设每次发出的乒乓球的运动路线固定不变,且落在中线上.在乒乓球运行时,设乒乓球与端点A的水平距离为x(米),与桌面的高度为y(米),运行时间为t(秒),经多次测试后,得到如下部分数据:
某乒乓球馆使用发球机进行辅助训练,出球口在桌面中线端点A处的正上方,假设每次发出的乒乓球的运动路线固定不变,且落在中线上.在乒乓球运行时,设乒乓球与端点A的水平距离为x(米),与桌面的高度为y(米),运行时间为t(秒),经多次测试后,得到如下部分数据:| t(秒) | 0 | 0.16 | 0.2 | 0.4 | 0.6 | 0.64 | 0.8 | 6 |
| X(米) | 0 | 0.4 | 0.5 | 1 | 1.5 | 1.6 | 2 | … |
| y(米) | 0.25 | 0.378 | 0.4 | 0.45 | 0.4 | 0.378 | 0.25 | … |
(2)乒乓球落在桌面时,与端点A的水平距离是多少?
(3)乒乓球落在桌面上弹起后,y与x满足y=a(x-3)2+k.
①用含a的代数式表示k;
②球网高度为0.14米,球桌长(1.4×2)米.若球弹起后,恰好有唯一的击球点,可以将球沿直线恰好擦网扣杀到A,求a的值.
1.给出四个数0,$\sqrt{3},\;\frac{1}{2}$,-1,其中最小的是( )
| A. | 0 | B. | $\sqrt{3}$ | C. | $\frac{1}{2}$ | D. | -1 |
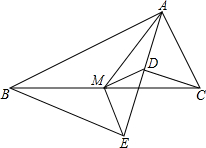 如图,Rt△ABC中,分别以AB、AC为斜边,向△ABC的内侧作等腰Rt△ABE、Rt△ACD,点M是BC的中点,连接MD、ME.
如图,Rt△ABC中,分别以AB、AC为斜边,向△ABC的内侧作等腰Rt△ABE、Rt△ACD,点M是BC的中点,连接MD、ME.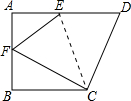 如图,四边形ABCD中,AD∥BC,∠B=90°,将四边形ABCD沿CE折叠,使点D落在AB上的F点.若AB=BC=6,EF=5,∠FCD=90°,则AF长度为3或4.
如图,四边形ABCD中,AD∥BC,∠B=90°,将四边形ABCD沿CE折叠,使点D落在AB上的F点.若AB=BC=6,EF=5,∠FCD=90°,则AF长度为3或4. 如图,已知△ABC中,∠C=90°,AC=BC=$\sqrt{2}$,将△ABC绕点A按顺时针方向旋转60°到△ADE的位置,连接BD并延长交AE于F.
如图,已知△ABC中,∠C=90°,AC=BC=$\sqrt{2}$,将△ABC绕点A按顺时针方向旋转60°到△ADE的位置,连接BD并延长交AE于F.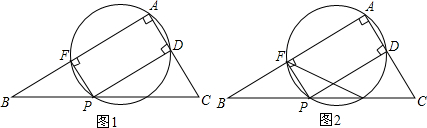
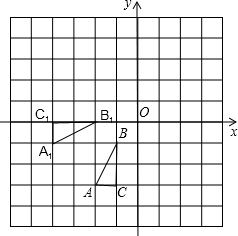 如图,每个小方格都是边长为1个单位长度的正方形,△ABC和△A1B1C1在平面直角坐标系中位置如图所示.
如图,每个小方格都是边长为1个单位长度的正方形,△ABC和△A1B1C1在平面直角坐标系中位置如图所示.