题目内容
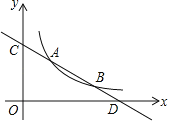
【题目】已知抛物线![]() 交x轴于A、B两点,其中点A坐标为
交x轴于A、B两点,其中点A坐标为![]() ,与y轴交于点C,且对称轴在y轴的左侧,抛物线的顶点为P.
,与y轴交于点C,且对称轴在y轴的左侧,抛物线的顶点为P.
(1)当![]() 时,求抛物线的顶点坐标;
时,求抛物线的顶点坐标;
(2)当![]() 时,求b的值;
时,求b的值;
(3)在(1)的条件下,点Q为x轴下方抛物线上任意一点,点D是抛物线对称轴与x轴的交点,直线![]() 、
、![]() 分别交抛物线的对称轴于点M、N.请问
分别交抛物线的对称轴于点M、N.请问![]() 是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
【答案】(1)![]() .(2)
.(2)![]() .(3)
.(3)![]() ,为定值
,为定值
【解析】
(1)将![]() ,A坐标
,A坐标![]() 代入抛物线解析式即可;
代入抛物线解析式即可;
(2)设B点坐标为![]() ,可证明
,可证明![]() 是等腰直角三角形,通过勾股定理即可求得
是等腰直角三角形,通过勾股定理即可求得![]() 长度,即
长度,即![]() 的长,从而求得b的值.
的长,从而求得b的值.
(3)设![]() ,求得直线
,求得直线![]() ,直线
,直线![]() ,用含t的代数式表示
,用含t的代数式表示![]() 即可求解.
即可求解.
(1)∵![]() ,∴抛物线为
,∴抛物线为![]() ,
,
∴将点![]() 代入
代入![]() ,得
,得![]() ,∴
,∴![]() ,
,
∴抛物线的解析式为![]() ,
,
∴顶点坐标为![]() .
.
(2)由已知将点![]() 代入
代入![]() ,得
,得![]() ,∴
,∴![]() ,
,
∵对称轴在y轴的左侧,∴![]() ,
,
∴![]() ,∴
,∴![]() ;
;
设B点坐标为![]() ,则
,则![]() ∴
∴![]() ,
,
∴![]() ,
,![]() 是等腰直角三角形,
是等腰直角三角形,
∴由勾股定理得![]() ,
,
又∵![]() ,
,
∴![]() ,
,
解得![]() .
.
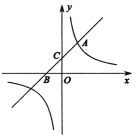
(3)![]() 为定值,如图所示:
为定值,如图所示:
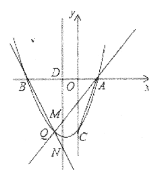
∵抛物线![]() 的对称轴为:直线
的对称轴为:直线![]()
∴![]() ,
,![]()
设![]()
设直线![]() 解析式为
解析式为![]()
∴![]() ,解得:
,解得:![]()
∴直线![]()
当![]() 时,
时,![]()
∴![]()
设直线![]() 解析式为
解析式为![]()
∴![]() 解得:
解得:![]()
∴直线![]()
当![]() 时,
时,![]()
∴![]()
∴![]() ,为定值.
,为定值.

 习题精选系列答案
习题精选系列答案【题目】某剧院举行专场音乐会,成人票每张20元,学生票每张5元.暑假期间,为了丰富广大师生的业余文化生活,影剧院制定了两种优惠方案,方案一:购买一张成人票赠送一张学生票;方案二:按总价的90%付款.某校有4名老师带队,与若干名(不少于4人)学生一起听音乐会.设学生人数为x人,![]() (x为整数).
(x为整数).
(Ⅰ)根据题意填表:
学生人数/人 | 4 | 10 | 20 | … |
方案一付款金额/元 | 80 | 110 | … | |
方案二付款金额/元 | 90 | 117 | … |
(Ⅱ)设方案一付款总金额为![]() 元,方案二付款总金额为
元,方案二付款总金额为![]() 元,分别求
元,分别求![]() ,
,![]() 关于x的函数解析式;
关于x的函数解析式;
(Ⅲ)根据题意填空:
①若用两种方案购买音乐会的花费相同,则听音乐会的学生有________________人;
②若有60名学生听音乐会,则用方案_______________购买音乐会票的花费少;
③若用一种方案购买音乐会票共花费了450元,则用方案________________购买音乐会票,使听音乐的学生人数多.