题目内容
1．如图，边长为（a+4）的正方形纸片剪出一个边长为a的正方形之后，剩余部分可剪拼成一个矩形（无缝隙，不重叠），若拼成的矩形一边长为4，则另一边长是（ ）
| A． | a+4 | B． | a+8 | C． | 2a+4 | D． | 2a+8 |
分析 由于边长为（a+4）的正方形纸片剪出一个边长为a的正方形之后，剩余部分又剪拼成一个矩形（不重叠无缝隙），那么根据正方形的面积公式，可以求出剩余部分的面积，而矩形一边长为4，利用矩形的面积公式即可求出另一边长．
解答 解：依题意得剩余部分面积为：（a+4）2-a2=a2+8a+16-a2=8a+16，
∵拼成的矩形一边长为4，
∴另一边长是（8a+16）÷4=2a+4．
故选C．
点评 本题主要考查平方差公式的几何背景，涉及了多项式除以单项式，解题关键是熟悉除法法则，难度一般．
练习册系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
11．
如图，一艘船由A港沿北偏西60°方向航行10海里至B港，然后再沿北偏东30°方向航行10海里至C港．则下列说法正确的是（ ）
如图，一艘船由A港沿北偏西60°方向航行10海里至B港，然后再沿北偏东30°方向航行10海里至C港．则下列说法正确的是（ ）| A． | C港在A港的南偏西30°方向上 | B． | C港在A港的北偏西30°方向上 | ||
| C． | C港在A港的北偏西15°方向上 | D． | C港在A港的南偏西15°方向上 |
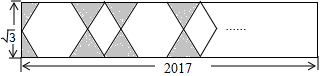
12．如图，在宽为$\sqrt{3}$的矩形纸条上进行剪裁，剪去阴影部分的三角形，使得剩下的正六边形和菱形依次相连，相连顶点处菱形的内角为120°．若该纸条的长为2017，则多余的小矩形的宽度y为1．
16．
如图，在半径为5的⊙O中，OP⊥AB，垂足为P，OP=3，则弦AB的长为（ ）
如图，在半径为5的⊙O中，OP⊥AB，垂足为P，OP=3，则弦AB的长为（ ）| A． | 5 | B． | 6 | C． | 7 | D． | 8 |
6．
在菱形ABCD中，对角线AC、BD相交于点O，AC=8，BD=6，则菱形ABCD的周长是（ ）
在菱形ABCD中，对角线AC、BD相交于点O，AC=8，BD=6，则菱形ABCD的周长是（ ）| A． | 20 | B． | 40 | C． | 24 | D． | 48 |
3．小强买了一张100元的乘车IC卡，如果用x表示他乘车的次数，那么卡内的余额y（元）如表所示：
（1）写出余额y与乘车的次数x的关系式；
（2）利用上述关系式计算小强乘了25次车后，卡内的余额还有多少元？
（3）小强用这张IC卡最多能乘多少次车？
| 次数 x | 余额 y（元） |
| 1 | 100-1.6 |
| 2 | 100-3.2 |
| 3 | 100-4.8 |
| 4 | 100-6.4 |
| … | … |
（2）利用上述关系式计算小强乘了25次车后，卡内的余额还有多少元？
（3）小强用这张IC卡最多能乘多少次车？