题目内容
17.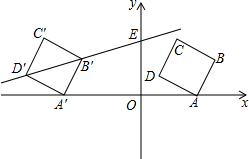 如图,在平面直角坐标系中,四边形ABCD为正方形,A(3,0),D(1,1),点B,C在第一象限内.
如图,在平面直角坐标系中,四边形ABCD为正方形,A(3,0),D(1,1),点B,C在第一象限内.(1)求点B的坐标;
(2)将正方形ABCD以每秒1个单位的速度沿x中向左平移,设运动时间为t秒,若存在某一时刻t,使在第二象限内点B,D两点的对应点B′、D′所在直线与y轴交于点E,并且OE=OA,请求出此时t的值以及直线B′D′的解析式;
(3)在(2)的条件下,求出点B′、D′的坐标.
分析 (1)作BM⊥x轴于M,DN⊥x轴于N,先证得△ADN≌△ABM,得出AM=DN,BM=AN,根据A(3,0),D(1,1)得出ON=1,DN=1,OA=3,进而得出OM=4,BM=2,AN=2,从而求得B的坐标.
(2)根据B、D的坐标,利用待定系数法即可求得直线BD的斜率k=$\frac{1}{3}$,然后根据题意即可得出直线B′D′的解析式为y=$\frac{1}{3}$x+3;根据平移的性质,根据B、D的坐标得出B′(4-t,2),D′(1-t,1),代入直线B′D′的解析式即可求得t的值.
(3)根据B′(4-t,2),D′(1-t,1),和t的值即可求得点B′、D′的坐标.
解答 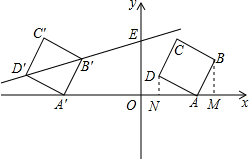 解:(1)作BM⊥x轴于M,DN⊥x轴于N,
解:(1)作BM⊥x轴于M,DN⊥x轴于N,
∵∠DAB=90°,
∴∠DAN+∠BAM=90°,
∴∠DAN=∠ABM,
在△ADN和△ABM中,
$\left\{\begin{array}{l}{∠DAN=∠ABM}\\{∠AND=∠AMB=90°}\\{AD=AB}\end{array}\right.$,
∴△ADN≌△ABM(AAS),
∴AM=DN,BM=AN,
∵A(3,0),D(1,1),
∴ON=1,DN=1,OA=3,
∴AN=2,
∴OM=4,BM=2,
∴B(4,2).
(2)∵B(4,2),D(1,1),
设直线BD的解析式为y=kx+b,
∴$\left\{\begin{array}{l}{k+b=1}\\{4k+b=2}\end{array}\right.$,
解得k=$\frac{1}{3}$,
∵正方形ABCD以每秒1个单位的速度沿x轴向左平移,且OE=OA,
∴直线B′D′的解析式为y=$\frac{1}{3}$x+3,
B′(4-t,2),D′(1-t,1),
∴1=$\frac{1}{3}$(1-t)+3,解得t=7,
(3)∵t=7,B′(4-t,2),D′(1-t,1),
∴B(-3,2),D(-6,1).
点评 本题是一次函数的综合题,考查了三角形全等的判定和性质,待定系数法求一次函数的解析式,平移的性质,平行线的性质等,熟悉两条平行线的斜率相等是解题的关键.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案| A. | 1.25×107 | B. | 1.25×108 | C. | 12.5×109 | D. | 0.0125×1010 |
| A. | (-$\frac{2}{3}$,3) | B. | (-$\frac{3}{2}$,-2) | C. | (3,-1) | D. | (-2,-$\frac{3}{2}$) |
 如图所示,点A的坐标为(2,1),点B的坐标为(5,3),点C为x轴上一动点,则AC+BC的最小值为5.
如图所示,点A的坐标为(2,1),点B的坐标为(5,3),点C为x轴上一动点,则AC+BC的最小值为5.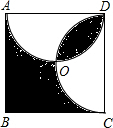 如图,分别以正方形ABCD的边AD和DC为直径画两个半圆交于点O,若正方形的边长为10cm,求阴影部分的面积.
如图,分别以正方形ABCD的边AD和DC为直径画两个半圆交于点O,若正方形的边长为10cm,求阴影部分的面积.