题目内容
4.化简:($\frac{{x}^{-2}-{y}^{-2}}{{x}^{-1}-{y}^{-1}}$)2•(x-1+y-1)-2.分析 根据负整数指数幂的计算法则进行计算即可.
解答 解:原式=($\frac{\frac{1}{{x}^{2}}-\frac{1}{{y}^{2}}}{\frac{1}{x}-\frac{1}{y}}$)2•($\frac{1}{x}$+$\frac{1}{y}$)-2
=($\frac{\frac{(y-x)(y+x)}{{x}^{2}{y}^{2}}}{\frac{y-x}{xy}}$)2•($\frac{1}{x}$+$\frac{1}{y}$)-2
=$\frac{(y+x)^{2}}{{x}^{2}{y}^{2}}$•$\frac{{x}^{2}{y}^{2}}{(y+x)^{2}}$
=1.
点评 本题考查的是负整数指数幂,熟知负整数指数幂的计算法则是解答此题的关键.

练习册系列答案
相关题目
 如图所示,点A的坐标为(2,1),点B的坐标为(5,3),点C为x轴上一动点,则AC+BC的最小值为5.
如图所示,点A的坐标为(2,1),点B的坐标为(5,3),点C为x轴上一动点,则AC+BC的最小值为5.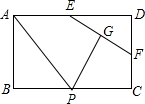 如图,矩形ABCD中,AB=2,AD=3,点E、F分别AD、DC边上的点,且EF=2,点G为EF的中点,点P为BC上一动点,则PA+PG的最小值为4.
如图,矩形ABCD中,AB=2,AD=3,点E、F分别AD、DC边上的点,且EF=2,点G为EF的中点,点P为BC上一动点,则PA+PG的最小值为4.
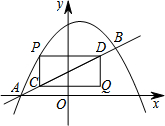 如图,抛物线$y=-\frac{1}{2}{x^2}+bx+c$与直线$y=\frac{1}{2}x+1$交于A、B两点,点A在x轴上,点B的横坐标是2.点P在直线AB上方的抛物线上,过点P分别作PC∥y轴、PD∥x轴,与直线AB交于点C、D,以PC、PD为边作矩形PCQD,设点Q的坐标为(m,n).
如图,抛物线$y=-\frac{1}{2}{x^2}+bx+c$与直线$y=\frac{1}{2}x+1$交于A、B两点,点A在x轴上,点B的横坐标是2.点P在直线AB上方的抛物线上,过点P分别作PC∥y轴、PD∥x轴,与直线AB交于点C、D,以PC、PD为边作矩形PCQD,设点Q的坐标为(m,n).