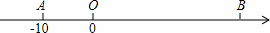题目内容
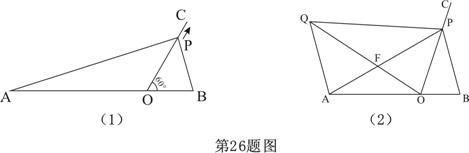
如图(1),线段AB与射线OC相交于点O,且∠BOC=60°,AO=3,OB=1,动点P以每秒1个单位长度的速度从点O出发,在射线OC做匀速运动,设运动时间为t秒.
(1)当t=3秒时,则OP= ,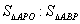 = ;
= ;
(2)当△OPB是直角三角形时,求t的值;
(3)如图(2),当AP=AB,过点A作AQ∥BP,并使得∠QOP=∠B,连接QP,QO、AP交于点F,试证明△APQ∽△BPO。
解:(1)OP=3,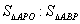 =3:4 4分
=3:4 4分
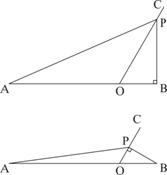 (2)①∵∠BOP=60°∴∠BOP不为直角; 5分
(2)①∵∠BOP=60°∴∠BOP不为直角; 5分
②当∠OBP=90°时,如图所示
∵∠BOP=60°∴∠OPB=30°
∴OP=2OB,
∴t=2s 7分
③当∠OPB=90°时,如图所示
∵∠BOP=60°∴∠OBP=30°
∴OB=2OP,
∴2t=1 ∴t=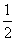 s 8分
s 8分
综上,当△OPB为直角三角形时,t=2s或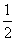 s 9分
s 9分
(3) ∵AQ∥BP,
∴ ∠QAP=∠APB
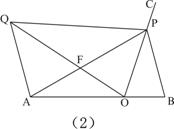 ∵ AP=AB
∵ AP=AB
∴∠APB=∠B ∴ ∠QAP=∠B
又∵ ∠QOP=∠B
∴ ∠QAP=∠QOP
又∵∠QFA=∠PFO
∴ △QFA∽△PFO
∴ 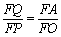 , 11分
, 11分
即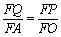 12分
12分
又∵ ∠PFQ=∠OFA,
∴ △PFQ∽△OFA 13分
∴ ∠QPA=∠QOA.
∵ ∠AOC=∠OPB+∠B=∠QOA+∠QOP,∠B=∠QOP,
∴∠QOA=∠OPB ∴∠OPB =∠QPA.
∴ △APQ∽△BPO.

 阅读快车系列答案
阅读快车系列答案 的一元二次方程
的一元二次方程 根的情况是( )
根的情况是( )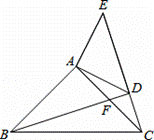
 上有两点A(
上有两点A( ,
, ),B(
),B( ,
, ),且
),且 ,则
,则 B.
B. C.
C. D.无法确定
D.无法确定