题目内容
3.已知多项式(2nab3+nab+ma2b)-(mab3+ab-2a2b)是关于a、b的四次二项式,且单项式2a5-mb3n与该多项式的次数相同,求m2+n2.分析 先合并同类项,根据题意得到2n-m≠0,n-1=0或m+2=0,依此求出m,n,再代入计算即可求解.
解答 解:原式=(2n-m)ab3+(n-1)ab+(m+2)a2b,
∵多项式(2nab3+nab+ma2b)-(mab3+ab-2a2b)是关于a、b的四次二项式,
∴2n-m≠0,n-1=0或m+2=0,
当n-1=0,n=1时,m=4,m2+n2=17,
当m+2=0,m=-2时,n=-1,
此时,2n-m=0,不符合题意.
点评 此题考查了多项式,单项式,合并同类项,关键是熟练掌握计算法则正确进行计算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.一个图形经过旋转,有以下结论:①图形的形状、大小不变;②对应线段相等;③对应线段平行;④旋转角相等,其中正确的结论是( )
| A. | ①②③ | B. | ①②④ | C. | ②③④ | D. | ①③④ |

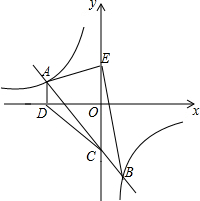 如图,一次函数y=ax+b(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于第二象限的点A(m,1),且与y轴交于点C.过点A作x轴的垂线,垂足为点D,连接CD,已知△ADC的面积为$\frac{3}{2}$,且tan∠ACO=1.
如图,一次函数y=ax+b(a≠0)的图象与反比例函数y=$\frac{k}{x}$(k≠0)的图象交于第二象限的点A(m,1),且与y轴交于点C.过点A作x轴的垂线,垂足为点D,连接CD,已知△ADC的面积为$\frac{3}{2}$,且tan∠ACO=1.