题目内容
14.计算:(1)3$\sqrt{3}$-($\sqrt{12}$+$\sqrt{\frac{1}{3}}$)
(2)(1-2$\sqrt{3}$)(1+2$\sqrt{3}$)-($\sqrt{3}$-1)2.
分析 (1)先把各二次根式化为最简二次根式,然后去括号后合并即可;
(2)利用平方差公式和完全平方公式进行计算.
解答 解:(1)原式=3$\sqrt{3}$-2$\sqrt{3}$-$\frac{\sqrt{3}}{3}$
=$\frac{2\sqrt{3}}{3}$;
(2)原式=1-12-(3-2$\sqrt{3}$+1)
=-11-4+2$\sqrt{3}$
=-15+2$\sqrt{3}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
相关题目
4.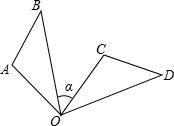 如图,△OAB绕点O顺时针旋转85°到△OCD,已知∠A=110°,若∠D=40°,则∠α的度数是( )
如图,△OAB绕点O顺时针旋转85°到△OCD,已知∠A=110°,若∠D=40°,则∠α的度数是( )
 如图,△OAB绕点O顺时针旋转85°到△OCD,已知∠A=110°,若∠D=40°,则∠α的度数是( )
如图,△OAB绕点O顺时针旋转85°到△OCD,已知∠A=110°,若∠D=40°,则∠α的度数是( )| A. | 30° | B. | 45° | C. | 55° | D. | 60° |
2.下列方程是一元二次方程的是( )
| A. | x2-2x=7 | B. | 3x-y=1 | C. | xy-4=0 | D. | x+$\frac{1}{x}$=1 |
19.下列事件:(1)打开电视机,正在播放新闻;(2)太阳每天从东方升起;(3)在操场上,抛出的铅球会下落;(4)随意掷一枚均匀的硬币两次,至少有一次反面朝上.其中确定事件的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
6.三角形的三个内角的度数的比为1:2:3,则这个三角形的形状为( )
| A. | 钝角三角形 | B. | 锐角三角形 | C. | 直角三角形 | D. | 不能确定 |