Question

9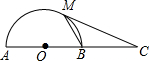．如图，AB为⊙O的直径，P点在AB延长线上，PM切⊙O于M点，若OA=a，PM=$\sqrt{3}$a，那么△PMB的周长为（　　）

• A． 2a
• B． 2$\sqrt{3}$a
• C． a
• D． （2+$\sqrt{3}$）a

Answer 1

分析 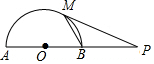首先连接OM，由PM切⊙O于M点，若OA=a，PM=$\sqrt{3}$a，可求得OP的长，继而求得BP的长，即可得OB=BP，利用直角三角形斜边上的中线等于斜边的一半，可求得BM的长，则可求得△PMB的周长．

解答 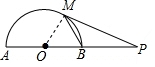解：连接OM，
∵PM切⊙O于M点，
∴OM⊥PM，
∴∠OMP=90°，
∵OM=OA=a，PM=$\sqrt{3}$a，
∴OP=$\sqrt{O{M}^{2}+P{M}^{2}}$=2a，
∵OB=OA=a，
∴BP=OP-OB=2a-a=a，
∴OB=$\frac{1}{2}$OP=OM，
∴MB=$\frac{1}{2}$OP=a，
∴△PMB的周长为：BM+BP+PM=a+a+$\sqrt{3}$a=（2+$\sqrt{3}$）a．
故选D．

点评 此题考查了切线的性质以及直角三角形的性质．注意准确作出辅助线是解此题的关键．