题目内容
4.计算:(1)(-1)2+tan45°-$\sqrt{4}$;
(2)已知$\frac{x}{y}$=$\frac{2}{3}$,求$\frac{3x-y}{x+2y}$的值.
分析 (1)分别根据数的乘方法则、特殊角的三角函数值及数的开方法则计算出各数,再根据实数混合运算的法则进行计算即可;
(2)用y表示出x的值,代入代数式进行计算即可.
解答 解:(1)原式=1+1-2=0;
(2)∵$\frac{x}{y}$=$\frac{2}{3}$,
∴x=$\frac{2}{3}$y,
∴原式=$\frac{3×\frac{2}{3}y-y}{\frac{2}{3}y+2y}$=$\frac{3}{8}$.
点评 本题考查的是比例的性质,熟知内项之积等于外项之积是解答此题的关键.

练习册系列答案
相关题目
14.一个多边形的每个外角是60°,则该多边形边数是( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
19.已知圆锥的底面半径为5,母线长为8,则这个圆锥的侧面积是( )
| A. | 13π | B. | 20π | C. | 40π | D. | 200π |
9.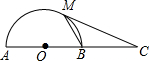 如图,AB为⊙O的直径,P点在AB延长线上,PM切⊙O于M点,若OA=a,PM=$\sqrt{3}$a,那么△PMB的周长为( )
如图,AB为⊙O的直径,P点在AB延长线上,PM切⊙O于M点,若OA=a,PM=$\sqrt{3}$a,那么△PMB的周长为( )
 如图,AB为⊙O的直径,P点在AB延长线上,PM切⊙O于M点,若OA=a,PM=$\sqrt{3}$a,那么△PMB的周长为( )
如图,AB为⊙O的直径,P点在AB延长线上,PM切⊙O于M点,若OA=a,PM=$\sqrt{3}$a,那么△PMB的周长为( )| A. | 2a | B. | 2$\sqrt{3}$a | C. | a | D. | (2+$\sqrt{3}$)a |
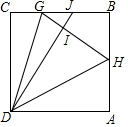 正方形ABCD中,∠GDH=45°,DI⊥GH并延长交BC于点J,GJ=5,GH=I0,求DJ长.
正方形ABCD中,∠GDH=45°,DI⊥GH并延长交BC于点J,GJ=5,GH=I0,求DJ长. 如图,梯形ABCD中,AD∥BC,EF分别是AB、CD的中点,线段EF交AC、BD于M、N两点,MN=1,AD<BC,且AD、BC的长是抛物线y=x2-2kx+k2-k+2与x轴两个交点的横坐标.
如图,梯形ABCD中,AD∥BC,EF分别是AB、CD的中点,线段EF交AC、BD于M、N两点,MN=1,AD<BC,且AD、BC的长是抛物线y=x2-2kx+k2-k+2与x轴两个交点的横坐标.