题目内容
已知反比例函数y=
的图象位于第一象限,在这个函数图象上取任意点A(x1,y1),B(x2,y2),如果y1>y2,那么x1与x2有怎样的大小关系?
w-
| ||
| x |
考点:反比例函数图象上点的坐标特征
专题:计算题
分析:根据反比例函数的性质得w-
>0,再根据反比例函数图象上点的坐标特征得到x1=
>0,x2=
>0,然后利用y1>y2,即可得到x1与x2的大小关系.
| 2 |
w-
| ||
| y1 |
w-
| ||
| y2 |
解答:解:∵反比例函数y=
的图象位于第一象限,
∴w-
>0,
∵点A(x1,y1),B(x2,y2)在反比例函数图象上,
∴x1•y1=x2•y2=w-
,
∴x1=
>0,x2=
>0,
∵y1>y2,
∴x1<x2.
w-
| ||
| x |
∴w-
| 2 |
∵点A(x1,y1),B(x2,y2)在反比例函数图象上,
∴x1•y1=x2•y2=w-
| 2 |
∴x1=
w-
| ||
| y1 |
w-
| ||
| y2 |
∵y1>y2,
∴x1<x2.
点评:本题考查了反比例函数图象上点的坐标特征:反比例函数y=
(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.
| k |
| x |

练习册系列答案
相关题目
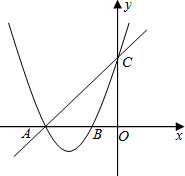 已知直线y=x+3与x轴、y轴分别交于点A、C,经过A、C两点的抛物线y=ax2+bx+c与x轴的另一交点为B,点B的横坐标为-1.
已知直线y=x+3与x轴、y轴分别交于点A、C,经过A、C两点的抛物线y=ax2+bx+c与x轴的另一交点为B,点B的横坐标为-1.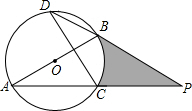 如图,AB是⊙O的直径,P是弦AC延长线上一点,且AC=CP,直线PB交⊙O于点D.
如图,AB是⊙O的直径,P是弦AC延长线上一点,且AC=CP,直线PB交⊙O于点D.