题目内容
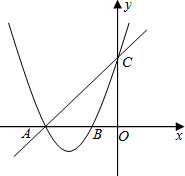 已知直线y=x+3与x轴、y轴分别交于点A、C,经过A、C两点的抛物线y=ax2+bx+c与x轴的另一交点为B,点B的横坐标为-1.
已知直线y=x+3与x轴、y轴分别交于点A、C,经过A、C两点的抛物线y=ax2+bx+c与x轴的另一交点为B,点B的横坐标为-1.(1)求该抛物线的解析式;
(2)求∠ACB的正切值;
(3)若点E是抛物线上一点,且∠EAB=∠ACB,求E点坐标.
考点:二次函数综合题
专题:
分析:(1)首先求出直线与坐标轴的交点坐标,进而利用交点式求出抛物线的解析式;
(2)利用勾股定理求出AC的长,再锐角三角函数关系求出即可;
(3)分别利用当E在x轴下方或当E在x轴上方,求出符合题意的答案.
(2)利用勾股定理求出AC的长,再锐角三角函数关系求出即可;
(3)分别利用当E在x轴下方或当E在x轴上方,求出符合题意的答案.
解答:解:(1)∵y=0,则0=x+3,解得;x=-3,当x=0,y=3,
∴A(-3,0),C(0,3),
∵B(-1,0),
∴设抛物线解析式为:y=a(x+1)(x+3),将(0,3)代入得出:
3=3a,
解得:a=1,
故抛物线解析为:y=(x+1)(x+3)=x2+4x+3;
(2)如图所示:过点B作BD⊥AC于点D,
∵A(-3,0),C(0,3),
∴AO=CO=3,
∴AC=
=3
,∠CAO=45°,
∴AD=BD,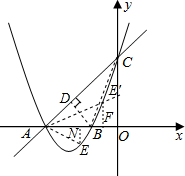
∵AO=3,BO=1,
∴AB=2,
∴AD=BD=
,
∴DC=2
,
∴tan∠ACB=
=
;
(3)如图所示:过点E作EN⊥AO于点N,过点E′作E′F⊥AO于点F,
当∠EAB=∠ACB时,
当E在x轴下方,则设E(x,x2+4x+3),
则AN=3+x,
NE=-(x2+4x+3),
故
=
=
,
解得:x1=-3(不合题意舍),x2=-
,
故x2+4x+3=-
,此时E(-
,-
);
当E在x轴上方,则设E(x,x2+4x+3),
则AF=3+x,
FE′=x2+4x+3,
故
=
=
,
解得:x1=-3(不合题意舍),x2=-
,
故x2+4x+3=
,此时E′(-
,
),
综上所述:E点坐标为:(-
,-
),(-
,
).
∴A(-3,0),C(0,3),
∵B(-1,0),
∴设抛物线解析式为:y=a(x+1)(x+3),将(0,3)代入得出:
3=3a,
解得:a=1,
故抛物线解析为:y=(x+1)(x+3)=x2+4x+3;
(2)如图所示:过点B作BD⊥AC于点D,
∵A(-3,0),C(0,3),
∴AO=CO=3,
∴AC=
| 32+32 |
| 2 |
∴AD=BD,

∵AO=3,BO=1,
∴AB=2,
∴AD=BD=
| 2 |
∴DC=2
| 2 |
∴tan∠ACB=
| BD |
| DC |
| 1 |
| 2 |
(3)如图所示:过点E作EN⊥AO于点N,过点E′作E′F⊥AO于点F,
当∠EAB=∠ACB时,
当E在x轴下方,则设E(x,x2+4x+3),
则AN=3+x,
NE=-(x2+4x+3),
故
| 1 |
| 2 |
| EN |
| AN |
| -x2-4x-3 |
| x+3 |
解得:x1=-3(不合题意舍),x2=-
| 3 |
| 2 |
故x2+4x+3=-
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 4 |
当E在x轴上方,则设E(x,x2+4x+3),
则AF=3+x,
FE′=x2+4x+3,
故
| 1 |
| 2 |
| E′F |
| AF |
| x2+4x+3 |
| x+3 |
解得:x1=-3(不合题意舍),x2=-
| 1 |
| 2 |
故x2+4x+3=
| 5 |
| 4 |
| 1 |
| 2 |
| 5 |
| 4 |
综上所述:E点坐标为:(-
| 3 |
| 2 |
| 3 |
| 4 |
| 1 |
| 2 |
| 5 |
| 4 |
点评:此题主要考查了二次函数综合以及锐角三角函数关系以及勾股定理等知识,利用分类讨论得出是解题关键.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
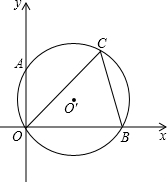 如图所示,已知CO、CB是⊙O′的弦,⊙O′与平面直角坐标系的x轴、y轴分别相交于点B、A,若∠COB=45°,∠OBC=75°,点A的坐标为(0,2),求⊙O′的直径.
如图所示,已知CO、CB是⊙O′的弦,⊙O′与平面直角坐标系的x轴、y轴分别相交于点B、A,若∠COB=45°,∠OBC=75°,点A的坐标为(0,2),求⊙O′的直径.