题目内容
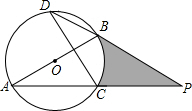 如图,AB是⊙O的直径,P是弦AC延长线上一点,且AC=CP,直线PB交⊙O于点D.
如图,AB是⊙O的直径,P是弦AC延长线上一点,且AC=CP,直线PB交⊙O于点D.(1)求证:CP=CD;
(2)若⊙O的直径是2,∠A=30°,求图中BC的长及阴影部分的面积.
考点:圆周角定理,扇形面积的计算
专题:
分析:(1)连接BC,则可知BC⊥AP,结合AC=PC,可得AB=BP,则∠A=∠P,结合图形得∠A=∠D,所以可得∠D=∠P,得出结论;
(2)在Rt△ABC中可求得BC,连接OC,可求得扇形OBC的面积,进一步求得弓形的面积,再利用△BCP的面积相减可求得阴影部分的面积.
(2)在Rt△ABC中可求得BC,连接OC,可求得扇形OBC的面积,进一步求得弓形的面积,再利用△BCP的面积相减可求得阴影部分的面积.
解答:(1)证明:如图1,连接BC,
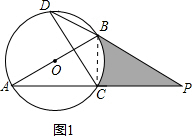
∵AB为直径,
∴∠BCA=90°,且AC=CP,
∴△ABP为等腰三角形,
∴∠A=∠P,
又∵∠A=∠D,
∴∠P=∠D,
∴CP=CD;
(2)解:如图2,连接OC,
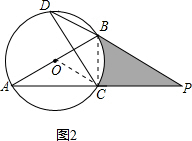
∵∠A=30°,
∴∠BOC=2∠A=60°,
∵AB=2,
∴BC=
AB=1,则AC=
,
∴S△ABC=
AC•BC=
×
×1=
,
∴S扇形BOC=
π×12=
,S△BOC=
S△ABC=
,
∴S弓形BOC=S扇形BOC-S△BOC=S扇形BOC=
-
,
∴S阴影=S△PCB-S弓形BOC=S△ABC-S弓形BOC=
-(
-
)=
-
.

∵AB为直径,
∴∠BCA=90°,且AC=CP,
∴△ABP为等腰三角形,
∴∠A=∠P,
又∵∠A=∠D,
∴∠P=∠D,
∴CP=CD;
(2)解:如图2,连接OC,

∵∠A=30°,
∴∠BOC=2∠A=60°,
∵AB=2,
∴BC=
| 1 |
| 2 |
| 3 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
∴S扇形BOC=
| 1 |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
| ||
| 4 |
∴S弓形BOC=S扇形BOC-S△BOC=S扇形BOC=
| π |
| 6 |
| ||
| 4 |
∴S阴影=S△PCB-S弓形BOC=S△ABC-S弓形BOC=
| ||
| 2 |
| π |
| 6 |
| ||
| 4 |
3
| ||
| 4 |
| π |
| 6 |
点评:本题主要考查圆周角定理及等腰三角形的性质、扇形面积的计算等,解题的关键是把阴影部分的面积化成规则图形的面积的和或差.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列变形正确的是( )
| A、从4x=2x-1可得到4x-2x=1 | ||||
B、从
| ||||
| C、从1-3(2x-1)=2x得1-6x-3=2x | ||||
| D、从-3x-2=2x+3得-3x-2x=3+2 |