题目内容
7. 如图,在△ABC中,AB=AC,∠A=80°,BD平分∠ABC,则∠BDC的度数为( )
如图,在△ABC中,AB=AC,∠A=80°,BD平分∠ABC,则∠BDC的度数为( )| A. | 100° | B. | 65° | C. | 75° | D. | 105° |
分析 由AB=AC,根据等腰三角形的性质得到∠ABC=∠C,再根据三角形内角和定理得到∠ABC=∠C=(180°-80°)÷2=50°,然后利用角平分线的定义求出∠DBC,最后根据三角形内角和定理可求出∠BDC.
解答 解:∵AB=AC,
∴∠ABC=∠C,
∵∠A=40°,
∴∠ABC=∠C=(180°-80°)÷2=50°,
而BD为∠ABC的平分线,
∴∠DBC=$\frac{1}{2}$×50°=25°,
∴∠BDC=180°-∠C-∠DBC=180°-50°-25°=105°.
故选D.
点评 本题考查了等腰三角形的性质:等腰三角形的两底角相等.也考查了三角形的内角和定理.

练习册系列答案
相关题目
18.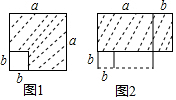 如图1,在长为a的正方形中挖掉一个边长为b的小正方形(a>b)把余下的部分剪拼成一个矩形(如图2),通过计算两个图形(阴影部分)的面积,验证了一个等式,则这个等式是( )
如图1,在长为a的正方形中挖掉一个边长为b的小正方形(a>b)把余下的部分剪拼成一个矩形(如图2),通过计算两个图形(阴影部分)的面积,验证了一个等式,则这个等式是( )
 如图1,在长为a的正方形中挖掉一个边长为b的小正方形(a>b)把余下的部分剪拼成一个矩形(如图2),通过计算两个图形(阴影部分)的面积,验证了一个等式,则这个等式是( )
如图1,在长为a的正方形中挖掉一个边长为b的小正方形(a>b)把余下的部分剪拼成一个矩形(如图2),通过计算两个图形(阴影部分)的面积,验证了一个等式,则这个等式是( )| A. | a2-b2=(a+b)(a-b) | B. | (a+b)2=a2+2ab 十b2 | ||
| C. | (a-b)2=a2-2ab+b2 | D. | (a+2b)(a-b)═a2+ab-2b2 |
2.做重复试验:抛掷一枚啤酒瓶盖1000次.经过统计得“凸面向上”的次数为420次,则可以由此估计抛掷这枚啤酒瓶盖出现“凸面向上”的概率约为( )
| A. | 0.22 | B. | 0.42 | C. | 0.50 | D. | 0.58 |
19.甲、乙两城市为了解决空气质量污染问题,对城市及其周边的环境污染进行了综合治理.在治理的过程中,环保部门每月初对两城市的空气质量进行监测,连续10个月的空气污染指数如图所示.其中,空气污染指数≤50时,空气质量为优;50<空气污染指数≤100时,空气质量为良;100<空气污染指数≤150时,空气质量为轻微污染.
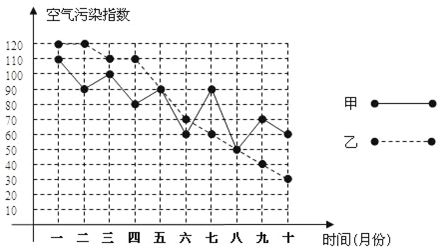
(1)填写下表:
(2)从以下四个方面对甲、乙两城市的空气质量进行分析.
①从平均数和空气质量为优的次数来分析:空气质量为优的次数甲城市比乙城市少;(填“多”或“少),乙城市的空气质量比甲城市的空气质量好些.(填“好些”或“差些”);
②从平均数和中位数来分析:甲的中位数<乙的中位数(填“=”、“>”或“<”),空气质量相对较好的城市是乙(填“甲”或“乙”);
③从平均数和方差来分析:S甲2<S乙2,空气污染指数比较稳定的城市是甲(填“甲”或“乙”);
④根据折线图上两城市的空气污染指数的走势来分析,两城市治理环境污染的效果较好的城市是乙(填“甲”或“乙”).

(1)填写下表:
| 平均数 | 方差 | 中位数 | 空气质量为优的次数 | |
| 甲 | 80 | 340 | 1 | |
| 乙 | 1060 | 80 | 3 |
①从平均数和空气质量为优的次数来分析:空气质量为优的次数甲城市比乙城市少;(填“多”或“少),乙城市的空气质量比甲城市的空气质量好些.(填“好些”或“差些”);
②从平均数和中位数来分析:甲的中位数<乙的中位数(填“=”、“>”或“<”),空气质量相对较好的城市是乙(填“甲”或“乙”);
③从平均数和方差来分析:S甲2<S乙2,空气污染指数比较稳定的城市是甲(填“甲”或“乙”);
④根据折线图上两城市的空气污染指数的走势来分析,两城市治理环境污染的效果较好的城市是乙(填“甲”或“乙”).
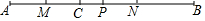 如图,点C是线段AB上一点,点M、N、P分别是线段AC、BC、AB的中点,AC=3cm,CP=1cm,求:
如图,点C是线段AB上一点,点M、N、P分别是线段AC、BC、AB的中点,AC=3cm,CP=1cm,求: