题目内容

3．已知直线l：y=x-3和点A（1，-2），B（-5，-8）．设P为l上一点，试判断P、A、B三点能否在同一个圆上．

分析 先根据一次函数图象上点的坐标特征判断点A、B都在直线y=x-3上，然后根据确定圆的条件即可判断P、A、B不在同一个圆上．

解答 解：当x=1时，y=x-3=-2，则点A（1，-2）在直线y=x-3上；
当x=-5时，y=x-3=-8，则点B（-5，-8）在直线y=x-3上，
而点P在直线y=x-3上，
所以点P、A、B不在同一个圆上．

点评 本题考查了一次函数图象上点的坐标特征：直线上任意一点的坐标都满足函数关系式y=kx+b．也考查了确定圆的条件．

练习册系列答案
相关题目
13．补全解答过程：
已知：如图，直线AB、CD相交于点O，OA平分∠EOC，若∠EOC：∠EOD=2：3，求∠BOD的度数．
解：由题意∠EOC：∠EOD=2：3，
设∠EOC=2x°，则∠EOD=3x°．
∵∠EOC+∠EOD=180°（平角的定义），
∴2x+3x=180．
x=36．
∴∠EOC=72°．
∵OA平分∠EOC（已知），
∴∠AOC=$\frac{1}{2}$∠EOC=36°．
∵∠BOD=∠AOC（对顶角相等），
∴∠BOD=36°（等量代换）
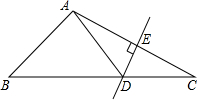14．如图：△ABC中，DE是AC的垂直平分线，AE=3cm，△ABD的周长为13cm，则△ABC的周长为19．
11．如图，四边形ABCD中，∠B=∠D=90°，
（1）图1中，点A，F，D在直线上，AF，CF分别是∠BAD和∠DCB的平分线，则AE与CF的位置关系是AE∥FC；
（2）图2中，点G、A、B在同-直线上，AE，CF分别是∠GAD和∠HCB的平分线，则AE与CF的位置关系是AE∥FC；
（3）图3中，点H，C，D在同-条直线上，AE，CF分别是∠BAD和∠HCB的平分线，则AE与CF的位置关系是AE⊥FC；
（4）请从（1）（2）（3）题中任选一个，证明你得出的结论．
18．计算：
（1）3+（-1）+（-3）+1+（-4）
（2）（-9）+4+（-5）+8
（3）（-36.35）+（-7.25）+26.35+（+7$\frac{1}{4}$）  
（4）$\frac{5}{9}$+1$\frac{5}{6}$+$\frac{4}{9}$+（-2）
（5）（-$\frac{3}{2}$）+（-$\frac{15}{12}$）+$\frac{5}{2}$+（-$\frac{7}{12}$）  
（6）（-$\frac{1}{3}$）+（+$\frac{2}{5}$）+（+$\frac{3}{5}$）+（-1$\frac{2}{3}$）
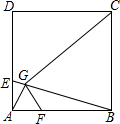8．如图，在正方形ABCD中，点E、F分别在边AD、AB上，且AE=AF，AG⊥BE于点G．求证：
（1）$\frac{AF}{AG}=\frac{BC}{BG}$；
（2）GF⊥GC．
15．已知a，b为有理数，且（3-2$\sqrt{3}$）2=a+b$\sqrt{3}$，求a+b的平方根．
9．如图，已知点M为?ABCD的边AB的中点，线段CM交BD于点E，则图中阴影部分的面积与?ABCD面积的比是（　　）
A．1：2B．2：5C．3：5D．1：3
10．有四张扑克牌，分别为红桃3，红桃4，红桃5，黑桃6，背面朝上洗匀后放在桌面上，从中任取一张后记下数字和颜色，再背面朝上洗匀，然后再从中随机取一张，两次都为红桃，并且数字之和不小于8的概率为$\frac{1}{3}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网