题目内容
2.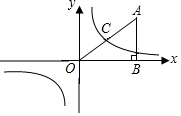 如图,AB⊥x轴于点B(8,0),sin∠AOB=$\frac{3}{5}$,反比例函数y1=$\frac{m}{x}$与OA相交于点C,且点C为OA的中点
如图,AB⊥x轴于点B(8,0),sin∠AOB=$\frac{3}{5}$,反比例函数y1=$\frac{m}{x}$与OA相交于点C,且点C为OA的中点(1)求反比例函数函数的解析式
(2)一次函数y2=x+4,当y2>y1时,直接写出x的取值范围.
分析 (1)过点C作CM⊥x轴,通过正弦函数得出AB的长,即可得出A的坐标,进而得出D的坐标,代入y1=$\frac{m}{x}$,根据待定系数法即可求得;
(2)根据图象求得即可.
解答 解:(1)过点C作CM⊥x轴,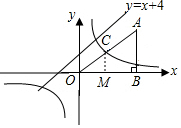
∵B(8,0),sin∠AOB=$\frac{3}{5}$,
∴AB=6,A(8,6),
又点C为OA的中点,
∴C(4,3),
∵点C在反比例函数y1=$\frac{m}{x}$上,
∴m=4×3=12,
∴反比例函数的解析式为y=$\frac{12}{x}$;
(2)解$\left\{\begin{array}{l}{y=\frac{12}{x}}\\{y=x+4}\end{array}\right.$得x=2或-6,
∵一次函数y2=x+4得图象过一、二、三象限,
∴当y2>y1时,x>2或-6<x<0.
点评 此题考查了反比例函数与一次函数的交点问题,锐角三角函数定义,以及坐标与图形性质,利用了待定系数法,待定系数法是常用的一种解题方法.同学们要熟练掌握这种方法.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
10.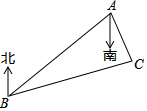 如图,C岛在A岛的南偏东15°方向,C岛在B岛的北偏东70°方向,从C岛看A、B两岛的视角∠ACB的度数是( )
如图,C岛在A岛的南偏东15°方向,C岛在B岛的北偏东70°方向,从C岛看A、B两岛的视角∠ACB的度数是( )
 如图,C岛在A岛的南偏东15°方向,C岛在B岛的北偏东70°方向,从C岛看A、B两岛的视角∠ACB的度数是( )
如图,C岛在A岛的南偏东15°方向,C岛在B岛的北偏东70°方向,从C岛看A、B两岛的视角∠ACB的度数是( )| A. | 95° | B. | 85° | C. | 60° | D. | 40° |
1. 下列图形中有可能与图相似的是( )
下列图形中有可能与图相似的是( )
 下列图形中有可能与图相似的是( )
下列图形中有可能与图相似的是( )| A. |  | B. |  | C. |  | D. |  |
2.下列计算正确的是( )
| A. | (-a3)2=-a6 | B. | 9a3÷3a3=3a3 | C. | 2a3+3a3=5a6 | D. | 2a3•3a2=6a5 |
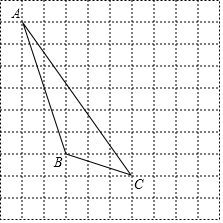 如图,在方格纸内将△ABC水平向右平移4个单位得到△A′B′C′.
如图,在方格纸内将△ABC水平向右平移4个单位得到△A′B′C′.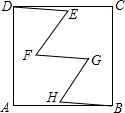 如图,在正方形ABCD中,点E,F,G,H均在其内部,且DE=EF=FG=GH=HB=1,∠E=∠F=∠G=∠H=60°,则AB=$\sqrt{7}$.
如图,在正方形ABCD中,点E,F,G,H均在其内部,且DE=EF=FG=GH=HB=1,∠E=∠F=∠G=∠H=60°,则AB=$\sqrt{7}$.