题目内容
17.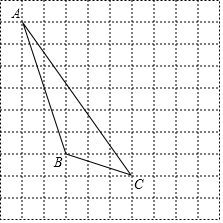 如图,在方格纸内将△ABC水平向右平移4个单位得到△A′B′C′.
如图,在方格纸内将△ABC水平向右平移4个单位得到△A′B′C′.(1)补全△A′B′C′,利用网格点和直尺画图;
(2)图中AC与A′C′的关系是:平行且相等;
(3)画出△ABC中AB边上的中线CE;
(4)平移过程中,线段AC扫过的面积是28.
分析 (1)根据图形平移的性质画出△A′B′C′即可;
(2)根据平移的性质可得出AC与A′C′的关系;
(3)先取AB的中点E,再连接CE即可;
(4)线段AC扫过的面积为平行四边形AA'C'C的面积,根据平行四边形的底为4,高为7,可得线段AC扫过的面积.
解答 解:(1)如图所示,△A′B′C′即为所求;
(2)由平移的性质可得,AC与A′C′的关系是平行且相等;
故答案为:平行且相等;
(3)如图所示,线段CE即为所求;
(4)如图所示,连接AA',CC',则线段AC扫过的面积为平行四边形AA'C'C的面积,
由图可得,线段AC扫过的面积=4×7=28.
故答案为:28.
点评 本题主要考查了利用平移变换进行作图,作图时要先找到图形的关键点,分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连接对应点即可得到平移后的图形.解题时注意:新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点,连接各组对应点的线段平行且相等.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
12. 如图,⊙O中,PC切⊙O于点C,连PO交于⊙O点A、B,点F是⊙O上一点,连PF,CD⊥AB于点D,AD=2,CD=4,则PF:DF的值是( )
如图,⊙O中,PC切⊙O于点C,连PO交于⊙O点A、B,点F是⊙O上一点,连PF,CD⊥AB于点D,AD=2,CD=4,则PF:DF的值是( )
 如图,⊙O中,PC切⊙O于点C,连PO交于⊙O点A、B,点F是⊙O上一点,连PF,CD⊥AB于点D,AD=2,CD=4,则PF:DF的值是( )
如图,⊙O中,PC切⊙O于点C,连PO交于⊙O点A、B,点F是⊙O上一点,连PF,CD⊥AB于点D,AD=2,CD=4,则PF:DF的值是( )| A. | 2 | B. | $\sqrt{5}$ | C. | 5:3 | D. | 4:3 |
17.已知点D与点A(0,8),B(0,-2),C(x,y)是平行四边形的四个顶点,其中x,y满足x-y+6=0,则CD长的最小值为( )
| A. | $\frac{16}{5}$ | B. | $3\sqrt{2}$ | C. | $2\sqrt{2}$ | D. | 10 |
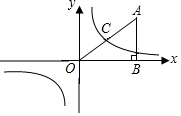 如图,AB⊥x轴于点B(8,0),sin∠AOB=$\frac{3}{5}$,反比例函数y1=$\frac{m}{x}$与OA相交于点C,且点C为OA的中点
如图,AB⊥x轴于点B(8,0),sin∠AOB=$\frac{3}{5}$,反比例函数y1=$\frac{m}{x}$与OA相交于点C,且点C为OA的中点 如图,DB为半圆的直径,A为BD延长线上一点,AC切半圆于点E,BC⊥AC于点C,交半圆于点F,已知BD=2,设AD=x,CF=y,求y关于x的函数解析式.
如图,DB为半圆的直径,A为BD延长线上一点,AC切半圆于点E,BC⊥AC于点C,交半圆于点F,已知BD=2,设AD=x,CF=y,求y关于x的函数解析式.