题目内容
11.(1)计算:$\frac{cos60°}{3sin30°-1}$+sin45°•cos45°(2)解方程:x2-5x-6=0.
分析 (1)代入特殊角的三角函数值,再计算即可求解;
(2)把方程左边进行因式分解得到(x-6)(x+1)=0,则方程就可化为两个一元一次方程x-6=0,或x+1=0,解两个一元一次方程即可.
解答 解:(1)$\frac{cos60°}{3sin30°-1}$+sin45°•cos45°
=$\frac{\frac{1}{2}}{\frac{3}{2}-1}$+($\frac{\sqrt{2}}{2}$)2
=1+$\frac{1}{2}$
=$\frac{3}{2}$;
(2)x2-5x-6=0
(x-6)(x+1)=0
解得x1=6,x2=-1.
点评 本题考查了特殊角的三角函数值,运用因式分解法解一元二次方程ax2+bx+c=0(a≠0)的方法:先把方程化为一般式,再把方程左边进行因式分解,然后一元二次方程就可化为两个一元一次方程,解两个一元一次方程即可.

练习册系列答案
相关题目
1.在△ABC中,BC=15cm,CA=45cm,AB=57cm,另一个和它相似的三角形的最短边长是5cm,则最长边长是
( )
( )
| A. | 18cm | B. | 19cm | C. | 24cm | D. | 19.5cm |
2.已知点P到∠AOB两边的距离相等,若∠POB=45°,则∠AOB等于( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
20.下列图形中既是中心对称图形又是轴对称图形的是( )
| A. | 等边三角形 | B. | 菱形 | C. | 平行四边形 | D. | 梯形 |
 北京紫禁城是中国古代汉族宫廷建筑之精华.经测算发现,太和殿,中和殿,保和殿这三大殿的矩形宫院ABCD(北至保和殿,南至太和门,西至弘义阁,东至体仁阁)与三大殿下的工字形大台基所在的矩形区域EFGH为相似形.若比较宫院与台基之间的比例关系,可以发现接近于9:5,取“九五至尊”之意.根据测量数据,三大殿台基的宽为40丈,请你估算三大殿宫院的宽为72丈.
北京紫禁城是中国古代汉族宫廷建筑之精华.经测算发现,太和殿,中和殿,保和殿这三大殿的矩形宫院ABCD(北至保和殿,南至太和门,西至弘义阁,东至体仁阁)与三大殿下的工字形大台基所在的矩形区域EFGH为相似形.若比较宫院与台基之间的比例关系,可以发现接近于9:5,取“九五至尊”之意.根据测量数据,三大殿台基的宽为40丈,请你估算三大殿宫院的宽为72丈. 如图,把一个长方形的纸ABCD沿对角线折叠(长方形对边平行且相等,四个角是直角),重合部分三角形FBD是什么图形?请证明你的结论.
如图,把一个长方形的纸ABCD沿对角线折叠(长方形对边平行且相等,四个角是直角),重合部分三角形FBD是什么图形?请证明你的结论.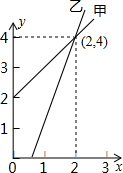 如图是甲、乙两家商店销售A种商品的销售价y(元)与销售量x(件)之间的函数的图象,请根据图象提供的信息,写出4个你认为正确的结论:
如图是甲、乙两家商店销售A种商品的销售价y(元)与销售量x(件)之间的函数的图象,请根据图象提供的信息,写出4个你认为正确的结论: