题目内容
13.解方程:$\frac{x+667}{2007}$=$\frac{x+1338}{2010}$-$\frac{669+x}{2013}$.分析 观察方程可得把分子整理为和分母的约数相关的式子化简后即可求得方程的解.
解答 解:$\frac{x-2+669}{2007}$=$\frac{x-2+1340}{2010}$-$\frac{x-2+671}{2013}$,
$\frac{x-2}{2007}$+$\frac{669}{2007}$=$\frac{x-2}{2010}$+$\frac{1340}{2010}$-$\frac{x-2}{2013}$-$\frac{671}{2013}$,
$\frac{x-2}{2007}$+$\frac{1}{3}$=$\frac{x-2}{2010}$+$\frac{2}{3}$-$\frac{x-2}{2013}$-$\frac{1}{3}$,
($\frac{1}{2007}$-$\frac{1}{2010}$+$\frac{1}{2013}$)(x-2)=0,
∵$\frac{1}{2007}$-$\frac{1}{2010}$+$\frac{1}{2013}$≠0,
∴x-2=0,
解得:x=2.
点评 此题考查了解一元一次方程,把分子整理为和分母的约数相关的式子化简原方程是解题的关键.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
4.在同圆中,圆心角∠AOB=2∠COD,则两条弦AB与CD关系是( )
| A. | AB=2CD | B. | AB=CD | C. | AB<2CD | D. | AB>2CD |
1.某单位要招聘1名英语翻译,张明参加招聘考试的成绩如表所示:
若把听、说、读、写的成绩按3:3:2:2计算平均成绩,则张明的平均成绩为( )
| 听 | 说 | 读 | 写 | |
| 张明 | 90 | 80 | 83 | 82 |
| A. | 82 | B. | 83 | C. | 84 | D. | 85 |
3.2016年3月份某省农产品实现出口额8 3620000美元.其中8 3620000用科学记数法表示为( )
| A. | 8.362×107 | B. | 83.62×106 | C. | 0.8362×108 | D. | 8.362×108 |
 按如图样式在日历上用一个斜框框出三个数,若三个数和为51,则这三天中的第一天是这个月的9号.
按如图样式在日历上用一个斜框框出三个数,若三个数和为51,则这三天中的第一天是这个月的9号. 自主学习,请阅读下列解题过程.
自主学习,请阅读下列解题过程. 如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-1,1),B(-3,1),C(-1,4).
如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-1,1),B(-3,1),C(-1,4).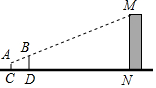 小亮想借助标杆测量教学楼的高度,他采用了下面的方法,先在楼前距离点N57m处直立一根高2m的标杆BD,然后他往后退,退到距离标杆3m的C处(点C,D,N在一条直线上)蹲下,通过调整眼睛离地面的高度,当楼的顶部M,标杆的顶部B及他的眼睛A恰好在同一条直线上时,让同伴量出眼睛与地面的距离AC为1m,根据上面的数据.你能帮小亮求出教学楼的高度吗?
小亮想借助标杆测量教学楼的高度,他采用了下面的方法,先在楼前距离点N57m处直立一根高2m的标杆BD,然后他往后退,退到距离标杆3m的C处(点C,D,N在一条直线上)蹲下,通过调整眼睛离地面的高度,当楼的顶部M,标杆的顶部B及他的眼睛A恰好在同一条直线上时,让同伴量出眼睛与地面的距离AC为1m,根据上面的数据.你能帮小亮求出教学楼的高度吗?