题目内容
13.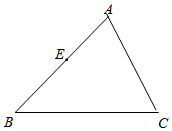 已知:如图,在△ABC中,过点A作AD⊥BC,垂足为D,E为AB上一点,过点E作EF⊥BC,垂足为F,过点D作DG∥AB交AC于点G.
已知:如图,在△ABC中,过点A作AD⊥BC,垂足为D,E为AB上一点,过点E作EF⊥BC,垂足为F,过点D作DG∥AB交AC于点G.(1)依题意补全图形;
(2)请你判断∠BEF与∠ADG的数量关系,并加以证明.
分析 (1)根据题意画出图形即可;
(2)证出AD∥EF,得出∠BEF=∠BAD,再由平行线的性质得出∠BAD=∠ADG,即可得出结论.
解答  (1)如图所示:
(1)如图所示:
(2)∠BEF=∠ADG.理由如下:
∵AD⊥BC,EF⊥BC,
∴∠ADF=∠EFB=90°.
∴AD∥EF(同位角相等,两直线平行).
∴∠BEF=∠BAD(两直线平行,同位角相等).
∵DG∥AB,
∴∠BAD=∠ADG(两直线平行,内错角相等).
∴∠BEF=∠ADG.
点评 本题考查了平行线的判定与性质;熟记平行线的判定与性质是关键,注意两者的区别.

练习册系列答案
相关题目
4.用配方法解方程x2-8x+15=0时,下列变形中,正确的是( )
| A. | (x-4)2=31 | B. | (x-4)2=1 | C. | (x-8)2=1 | D. | (x-8)2=31 |
1.菱形ABCD的一边中点M到对角线交点O的距离为2.5cm,则菱形ABCD的周长为( )
| A. | 5 cm | B. | 10 cm | C. | 20 cm | D. | 40 cm |
18.为了传承中华优秀传统文化,某校组织了一次七年级的“汉字听写”大赛,七年级1班学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,同学们把成绩进行整理,得到下列表格:
(1)七年级1班有50名学生;
(2)请选择一种统计图将整理的结果表示出来;
(3)七年级2班的成绩整理如下表:
请你谈谈哪个班的比赛成绩好些,并说明理由.
| 成绩(分) | 50 | 60 | 70 | 80 | 90 | 100 |
| 人数 | 2 | 6 | 9 | 18 | 13 | 2 |
(2)请选择一种统计图将整理的结果表示出来;
(3)七年级2班的成绩整理如下表:
| 成绩(分) | 50 | 60 | 70 | 80 | 90 | 100 |
| 人数 | 6 | 9 | 7 | 9 | 15 | 4 |
2.“勤劳”是中华民族的传统美德,我校要求同学们在家里帮助父母做些力所能及的家务.王刚同学在本学期开学初对部分同学寒假在家做家务的时间进行了抽样调查(时间取整数小时),所得数据统计如表:
(1)抽取样本的容量是100.
(2)根据表中数据补全图中的频数分布直方图.
(3)样本的中位数所在时间段的范围是40.5~60.5.
(4)若我学校共有学生1600人,那么大约有多少学生在寒假做家务的时间在40.5~100.5小时之间?
| 时间分组 | 0.5~20.5 | 20.5~40.5 | 40.5~60.5 | 60.5~80.5 | 80.5~100.5 |
| 频 数 | 20 | 25 | 30 | 15 | 10 |
(2)根据表中数据补全图中的频数分布直方图.
(3)样本的中位数所在时间段的范围是40.5~60.5.
(4)若我学校共有学生1600人,那么大约有多少学生在寒假做家务的时间在40.5~100.5小时之间?

3.如图所示的各组图形中,表示平移关系的是( )
| A. |  | B. |  | C. |  | D. |  |
 在平面直角坐标系中,△ABO的三个顶点坐标分别为:A(2,3)、B(3,1)、O(0,0).
在平面直角坐标系中,△ABO的三个顶点坐标分别为:A(2,3)、B(3,1)、O(0,0).