题目内容
1．三角形三条高的交点一定在（ ）| A． | 三角形内部 | B． | 三角形外部 | ||
| C． | 三角形内部或外部 | D． | 三角形内部、外部或顶点 |
分析 根据三角形的高线的定义分情况讨论高线的交点，即可得解．
解答 解：锐角三角形，三角形三条高的交点在三角形内部，
直角三角形，三角形三条高的交点在三角形直角顶点，
钝角三角形，三角形三条高的交点在三角形外部，
故选D．
点评 本题考查了三角形的高线，熟记三种三角形的高线的交点的位置是解题的关键．
练习册系列答案
相关题目
11．若关于x的方程$\frac{2}{x-1}$+$\frac{mx}{{x}^{2}-1}$=0有增根，则m的值为（ ）
| A． | 1 | B． | 0 | C． | -4 | D． | 0或-4 |
12．已知4x6ya÷32xby-2=$\frac{1}{8}$x2y3，那么（ ）
| A． | a=2，b=3 | B． | a=1，b=4 | C． | a=3，b=6 | D． | a=4，b=5 |
9．
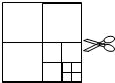如图，将一张正方形纸片剪成四个小正方形，得到4个小正方形，称为第一次操作；然后，将其中的一个正方形再剪成四个小正方形，共得到7个小正方形，称为第二次操作；再将其中的一个正方形再剪成四个小正方形，共得到10个小正方形，称为第三次操作；…，根据以上操作，若要得到2017个小正方形，则需要操作的次数是（ ）
如图，将一张正方形纸片剪成四个小正方形，得到4个小正方形，称为第一次操作；然后，将其中的一个正方形再剪成四个小正方形，共得到7个小正方形，称为第二次操作；再将其中的一个正方形再剪成四个小正方形，共得到10个小正方形，称为第三次操作；…，根据以上操作，若要得到2017个小正方形，则需要操作的次数是（ ）| A． | 672 | B． | 671 | C． | 670 | D． | 674 |
16．某款手机连续两次降价，由原来的1299元降到688元，设平均每次降价的百分数为x，则下面所列方程中正确的是（ ）
| A． | 688（1+x）2=1299 | B． | 1299（1+x）2=688 | C． | 688（1-x）2=1299 | D． | 1299（1-x）2=688 |
6．下列二次根式中，是最简二次根式的是（ ）
| A． | 2$\sqrt{3}$ | B． | $\sqrt{12}$ | C． | $\sqrt{\frac{1}{2}}$ | D． | $\sqrt{{x}^{4}+{x}^{3}{y}^{2}}$ |
13．已知正比例函数y=kx（k≠0）的图象经过点（1，3），则k的值为（ ）
| A． | 3 | B． | -3 | C． | $\frac{1}{3}$ | D． | $-\frac{1}{3}$ |
10．下列运算中，正确的是（ ）
| A． | x3÷x=x4 | B． | a2+a2=2a4 | C． | 3x-2x=1 | D． | 3x-2x=x |
11．直线y=-2x+1不经过第（ ）象限．
| A． | 一 | B． | 二 | C． | 三 | D． | 四 |