Question

18．（1）若O是锐角△ABC的外心，∠A=60°，则∠BOC=120°
（2）若O是钝角△ABC的外心，∠A=120°，则∠BOC=120°．

Answer 1

分析 （1）如图1中，根据圆周角定理，∠BOC=2∠A即可解决问题．
（2）如图2中，在优弧BC上取一点D，连接BD、CD，先根据∠A+∠D=180°，∠A=120°，求出∠D=60°，再根据∠BOC=2∠D即可解决问题．

解答 解：（1）如图1中，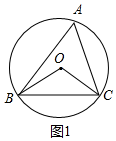

∵∠BOC=2∠A，∠A=60°，
∴∠BOC=120°，
故答案为120°

（2）如图2中，在优弧BC上取一点D，连接BD、CD，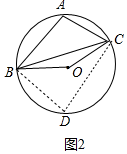

∵∠A+∠D=180°，∠A=120°，
∴∠D=60°，
∵∠BOC=2∠D，∠D=60°，
∴∠BOC=120°，
故答案为120°．

点评 本题考查三角形的外接圆与外心、圆内接四边形的性质、圆周角定理等知识，解题的关键是熟练应用这些知识解决问题，学会添加常用辅助线，属于中考常考题型．