题目内容
17. 如图,在正方形网格中,△ABC的顶点都在格点上,则tan∠ACB的值为$\frac{3}{5}$.
如图,在正方形网格中,△ABC的顶点都在格点上,则tan∠ACB的值为$\frac{3}{5}$.
分析 作AD⊥BC于D,利用勾股定理分别求出AC、AB、BC的长,根据三角形的面积公式求出AD、CD,根据正切的定义解答即可.
解答 解:作AD⊥BC于D,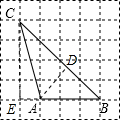 由勾股定理得,AC=$\sqrt{17}$,AB=3,BC=4$\sqrt{2}$,
由勾股定理得,AC=$\sqrt{17}$,AB=3,BC=4$\sqrt{2}$,
△ABC的面积为:$\frac{1}{2}$×AB×CE=6,
∴$\frac{1}{2}$×CB×AD=6,
解得AD=$\frac{3\sqrt{2}}{2}$,
CD=$\sqrt{A{C}^{2}-A{D}^{2}}$=$\frac{5\sqrt{2}}{2}$,
tan∠ACB=$\frac{AD}{CD}$=$\frac{3}{5}$.
故答案为:$\frac{3}{5}$.
点评 本题考查的是锐角三角函数的定义和勾股定理的应用,掌握锐角三角函数的定义是解题的关键.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
7.若m>n,t为任意实数,则下列各不等式中,恒成立的是( )
| A. | mt2>nt2 | B. | mt2≥nt2 | C. | mt>nt | D. | mt<nt |
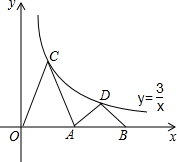 如图,点C、D在双曲线y=$\frac{3}{x}$(x>0)上,点A、B在x轴上,且OA=AB,CO=CA,DA=DB,则S△OCA+S△ADB=4.
如图,点C、D在双曲线y=$\frac{3}{x}$(x>0)上,点A、B在x轴上,且OA=AB,CO=CA,DA=DB,则S△OCA+S△ADB=4.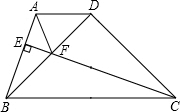 如图,在梯形ABCD中,AD∥BC,CE⊥AB于E,△BDC为等腰直角三角形,∠BDC=90°,BD=CD,CE与BD交于F,连接AF,求证:CF=AB+AF.
如图,在梯形ABCD中,AD∥BC,CE⊥AB于E,△BDC为等腰直角三角形,∠BDC=90°,BD=CD,CE与BD交于F,连接AF,求证:CF=AB+AF.