题目内容
14.先化简,再求值:2x2+3(-x2+3xy-y2)-(-x2-xy+2y2),其中x、y满足(2x-1)2+|y+2|=0.分析 原式去括号合并得到最简结果,利用非负数的性质求出x与y的值,代入计算即可求出值.
解答 解:原式=2x2-3x2+9xy-3y2+x2+xy-2y2=10xy-5y2,
∵(2x-1)2+|y+2|=0,
∴2x-1=0,y+2=0,
解得:x=$\frac{1}{2}$,y=-2,
则原式=-10-20=-30.
点评 此题考查了整式的加减-化简求值,以及非负数的性质,熟练掌握运算法则是解本题的关键.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
1.在Rt△ABC中,∠ACB=90°,BC=1,AB=2,则下列结论正确的是( )
| A. | $sinA=\frac{{\sqrt{3}}}{2}$ | B. | $cosA=\frac{{\sqrt{3}}}{2}$ | C. | $tanA=\frac{1}{2}$ | D. | $cotA=\frac{{\sqrt{3}}}{3}$ |
2.在?ABCD中,AB≠CD,满足下列条件,不一定能构成平行四边形的是( )
| A. | 四个内角平分线围成的四边形 | |
| B. | 过四个顶点作对边的高线围成的四边形 | |
| C. | 以各边中点为顶点的四边形 | |
| D. | 以一条对角线上的两点与另两个顶点为顶点的四边形 |
19.某校为了调查七年级450名学生的身高,随机抽取了该年级100名学生进行调查,下列说法中,错误的是( )
| A. | 总体是450名学生 | B. | 个体是每一名学生的身高 | ||
| C. | 样本是100名学生的身高 | D. | 样本容量是100 |
3.我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆.例如线段AB的最小覆盖圆就是以线段AB为直径的圆.若在△ABC中,AB=AC,BC=6,∠BAC=120°,则△ABC的最小覆盖圆的半径是( )
| A. | 3 | B. | $2\sqrt{3}$ | C. | 2 | D. | $3\sqrt{3}$ |
4. 如图,笑脸盖住的点的坐标可能为( )
如图,笑脸盖住的点的坐标可能为( )
 如图,笑脸盖住的点的坐标可能为( )
如图,笑脸盖住的点的坐标可能为( )| A. | (5,2) | B. | (3,-4) | C. | (-4,-6) | D. | (-1,3) |
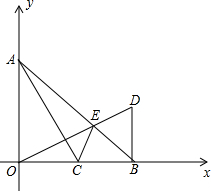 如图,在平面直角坐标系中,点A(0.4),B(4,0),C为OB的中点,连AC,OE⊥AC交AB于E,BD⊥x轴交OE的延长线于D.
如图,在平面直角坐标系中,点A(0.4),B(4,0),C为OB的中点,连AC,OE⊥AC交AB于E,BD⊥x轴交OE的延长线于D.