题目内容
17. 已知:线段AB.
已知:线段AB.(1)尺规作图:作线段AB的垂直平分线l,与线段AB交于点D;(保留作图痕迹,不写作法)
(2)在(1)的基础上,点C为l上一个动点(点C不与点D重合),连接CB,过点A作AE⊥BC,垂足为点E.
①当垂足E在线段BC上时,直接写出∠ABC度数的取值范围.
②请你画出一个垂足E在线段BC延长线上时的图形,并求证∠BAE=∠BCD.
分析 (1)利用作已知线段的垂直平分线的法作图即可;
(2)①根据锐角三角形的高在三角形内即可解决.
②利用等角的余角相等证明.
解答 解:(1)直线l即为所求作的直线.(见图1)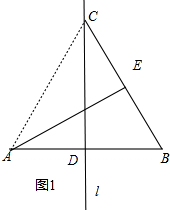
(2)①45°≤∠ABC<90°.
理由如下:连接AC,
当∠ACB≤90°时垂足E在线段BC上,
∵CD垂直平分AB,
∴CA=CB,
∴∠CAB=∠CBA,
∵2∠CBA+∠ACB=180°,
∴2∠CBA≥90°
∴∠CBA≥45°
∵∠CBA是锐角,
∴45°≤∠CBA<90°
②在图2中,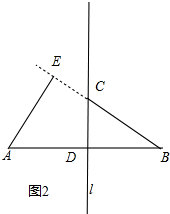
证明:∵线段AB的垂直平分线为l,
∴CD⊥AB,
∵AE⊥BE,
∴∠AEB=∠BDC=90°,
∴∠BAE+∠B=∠BCD+∠B=90°,
∴∠BAE=∠BCD.
点评 本题考查垂直平分线的作法、三角形的高、都等角的余角相等等知识,熟练掌握这些知识是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7. 如图,直线a∥b,AC⊥AB,AC交直线b于点C,∠ACB=65°,则∠1的度数是( )
如图,直线a∥b,AC⊥AB,AC交直线b于点C,∠ACB=65°,则∠1的度数是( )
 如图,直线a∥b,AC⊥AB,AC交直线b于点C,∠ACB=65°,则∠1的度数是( )
如图,直线a∥b,AC⊥AB,AC交直线b于点C,∠ACB=65°,则∠1的度数是( )| A. | 25° | B. | 35° | C. | 50° | D. | 65° |
5.下列各组中的两项,不是同类项的是( )
| A. | x2与2x | B. | 3a与2a | C. | -2x2y与yx2 | D. | 1与-5 |
 在寻找马航MH370的过程中,两艘搜救艇接到消息,在海面上有疑似漂浮目标A、B.于是,一艘搜救艇以16海里/时的速度离开港口O(如图)沿北偏东40°的方向向目标A的前进,同时,另一艘搜救艇也从港口O出发,以12海里/时的速度向着目标B出发,1.5小时后,他们同时分别到达目标A、B.此时,他们相距30海里,请问第二艘搜救艇的航行方向是北偏西多少度?
在寻找马航MH370的过程中,两艘搜救艇接到消息,在海面上有疑似漂浮目标A、B.于是,一艘搜救艇以16海里/时的速度离开港口O(如图)沿北偏东40°的方向向目标A的前进,同时,另一艘搜救艇也从港口O出发,以12海里/时的速度向着目标B出发,1.5小时后,他们同时分别到达目标A、B.此时,他们相距30海里,请问第二艘搜救艇的航行方向是北偏西多少度?