题目内容
11.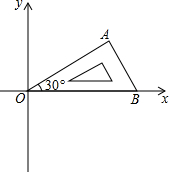 将含有30°角的直角三角板OAB如图放置在平面直角坐标系中,OB在x轴上,若OA=2,将三角板绕原点O顺时针旋转75°,则点A的对应点A′的坐标为( )
将含有30°角的直角三角板OAB如图放置在平面直角坐标系中,OB在x轴上,若OA=2,将三角板绕原点O顺时针旋转75°,则点A的对应点A′的坐标为( )| A. | ($\sqrt{3}$,-1) | B. | (1,-$\sqrt{3}$) | C. | ($\sqrt{2}$,-$\sqrt{2}$) | D. | (-$\sqrt{2}$,$\sqrt{2}$) |
分析 先根据题意画出点A′的位置,然后过点A′作A′C⊥OB,接下来依据旋转的定义和性质可得到OA′的长和∠COA′的度数,最后依据特殊锐角三角函数值求解即可.
解答 解:如图所示:过点A′作A′C⊥OB.
∵将三角板绕原点O顺时针旋转75°,
∴∠AOA′=75°,OA′=OA.
∴∠COA′=45°.
∴OC=2×$\frac{\sqrt{2}}{2}$=$\sqrt{2}$,CA′=2×$\frac{\sqrt{2}}{2}$=$\sqrt{2}$.
∴A′的坐标为($\sqrt{2}$,-$\sqrt{2}$).
故选:C.
点评 本题主要考查的是旋转的定义和性质、特殊锐角三角函数值的应用,得到∠COA′=45°是解题的关键.

练习册系列答案
相关题目
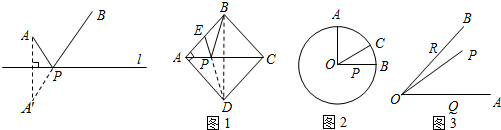
20. 如图,A、B、C是⊙O上的三点,∠B=75°,则∠AOC的度数是( )
如图,A、B、C是⊙O上的三点,∠B=75°,则∠AOC的度数是( )
 如图,A、B、C是⊙O上的三点,∠B=75°,则∠AOC的度数是( )
如图,A、B、C是⊙O上的三点,∠B=75°,则∠AOC的度数是( )| A. | 150° | B. | 140° | C. | 130° | D. | 120° |

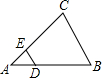 如图,在△ABC中,DE∥BC,DB=2AD,△ADE的面积为1,则四边形DBCE的面积为( )
如图,在△ABC中,DE∥BC,DB=2AD,△ADE的面积为1,则四边形DBCE的面积为( )
 如图,AB是半圆O的直径,点C、D是半圆O的三等分点,若弦CD=2,则图中阴影部分的面积为$\frac{2}{3}$π.
如图,AB是半圆O的直径,点C、D是半圆O的三等分点,若弦CD=2,则图中阴影部分的面积为$\frac{2}{3}$π. 如图,若要添加一条线段,使之既是轴对称图形又是中心对称图形,正确的添加位置是( )
如图,若要添加一条线段,使之既是轴对称图形又是中心对称图形,正确的添加位置是( )


