题目内容
20．
如图，A、B、C是⊙O上的三点，∠B=75°，则∠AOC的度数是（ ）| A． | 150° | B． | 140° | C． | 130° | D． | 120° |
分析 直接根据圆周角定理即可得出结论．
解答 解：∵A、B、C是⊙O上的三点，∠B=75°，
∴∠AOC=2∠B=150°．
故选A．
点评 本题考查的是圆周角定理，熟知在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半是解答此题的关键．
练习册系列答案
相关题目
11．
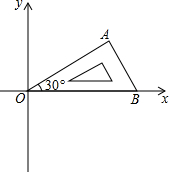将含有30°角的直角三角板OAB如图放置在平面直角坐标系中，OB在x轴上，若OA=2，将三角板绕原点O顺时针旋转75°，则点A的对应点A′的坐标为（ ）
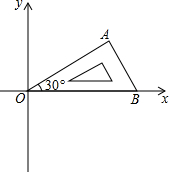将含有30°角的直角三角板OAB如图放置在平面直角坐标系中，OB在x轴上，若OA=2，将三角板绕原点O顺时针旋转75°，则点A的对应点A′的坐标为（ ）| A． | （$\sqrt{3}$，-1） | B． | （1，-$\sqrt{3}$） | C． | （$\sqrt{2}$，-$\sqrt{2}$） | D． | （-$\sqrt{2}$，$\sqrt{2}$） |
某班数学兴趣小组利用数学活动课时间测量位于烈山山顶的炎帝雕像高度，已知烈山坡面与水平面的夹角为30°，山高857.5尺，组员从山脚D处沿山坡向着雕像方向前进1620尺到达E点，在点E处测得雕像顶端A的仰角为60°，求雕像AB的高度．
5．
实数a，b在数轴上的对应点的位置如图所示，则正确的结论是（ ）
实数a，b在数轴上的对应点的位置如图所示，则正确的结论是（ ）| A． | a＞-2 | B． | a＜-3 | C． | a＞-b | D． | a＜-b |
9．一次数学考试中，九年（1）班和（2）班的学生数和平均分如表所示，则这两班平均成绩为82.6分．
| 班级 | 人数 | 平均分 |
| （1）班 | 52 | 85 |
| （2）班 | 48 | 80 |