题目内容
19.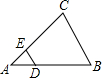 如图,在△ABC中,DE∥BC,DB=2AD,△ADE的面积为1,则四边形DBCE的面积为( )
如图,在△ABC中,DE∥BC,DB=2AD,△ADE的面积为1,则四边形DBCE的面积为( )| A. | 3 | B. | 5 | C. | 6 | D. | 8 |
分析 根据相似三角形的判定与性质,可得△ABC的面积,根据面积的和差,可得答案.
解答 解:由DE∥BC,DB=2AD,得
△ADE∽△ABC,$\frac{AD}{AB}$=$\frac{1}{3}$.
由,△ADE的面积为1,得
$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=$\frac{1}{9}$,
得S△ABC=9.
SDBCE=SABC-S△ADE=8,
故选:D.
点评 本题考查了相似三角形的判定与性质,利用相似三角形面积的比等于相似比的平方得出S△ABC=9是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.若k≠0,b<0,则y=kx+b的图象可能是( )
| A. |  | B. |  | C. |  | D. |  |
11.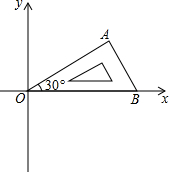 将含有30°角的直角三角板OAB如图放置在平面直角坐标系中,OB在x轴上,若OA=2,将三角板绕原点O顺时针旋转75°,则点A的对应点A′的坐标为( )
将含有30°角的直角三角板OAB如图放置在平面直角坐标系中,OB在x轴上,若OA=2,将三角板绕原点O顺时针旋转75°,则点A的对应点A′的坐标为( )
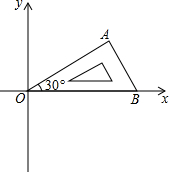 将含有30°角的直角三角板OAB如图放置在平面直角坐标系中,OB在x轴上,若OA=2,将三角板绕原点O顺时针旋转75°,则点A的对应点A′的坐标为( )
将含有30°角的直角三角板OAB如图放置在平面直角坐标系中,OB在x轴上,若OA=2,将三角板绕原点O顺时针旋转75°,则点A的对应点A′的坐标为( )| A. | ($\sqrt{3}$,-1) | B. | (1,-$\sqrt{3}$) | C. | ($\sqrt{2}$,-$\sqrt{2}$) | D. | (-$\sqrt{2}$,$\sqrt{2}$) |
9.一次数学考试中,九年(1)班和(2)班的学生数和平均分如表所示,则这两班平均成绩为82.6分.
| 班级 | 人数 | 平均分 |
| (1)班 | 52 | 85 |
| (2)班 | 48 | 80 |
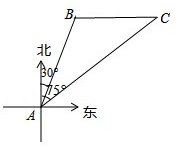 南海是我国的南大门,如图所示,某天我国一艘海监执法船在南海海域正在进行常态化巡航,在A处测得北偏东30°方向上,距离为20海里的B处有一艘不明身份的船只正在向正东方向航行,便迅速沿北偏东75°的方向前往监视巡查,经过一段时间后,在C处成功拦截不明船只,问我海监执法船在前往监视巡查的过程中行驶了多少海里(最后结果保留整数)?
南海是我国的南大门,如图所示,某天我国一艘海监执法船在南海海域正在进行常态化巡航,在A处测得北偏东30°方向上,距离为20海里的B处有一艘不明身份的船只正在向正东方向航行,便迅速沿北偏东75°的方向前往监视巡查,经过一段时间后,在C处成功拦截不明船只,问我海监执法船在前往监视巡查的过程中行驶了多少海里(最后结果保留整数)?