题目内容
7.比较两个数的大小时,我们可以用“比差法”,它的基本思路是:求出a与b两数的差:当a-b>0时,a>b;当a-b<0时,a<b;当a-b=0时,a=b.试运用“比差法”解决下列问题:(1)比较代数式2a+1与2(a+1)值的大小;
(2)比较代数式(a+b)与(a-b)值的大小.
分析 (1)利用作差法比较即可;
(2)分类讨论b的正负,利用作差法比较即可.
解答 解:(1)∵2a+1-2(a+1)=2a+1-2a-2=-1<0,
∴2a+1<2(a+1);
(2)(a+b)-(a-b)=a+b-a+b=2b,
当b>0时,a+b>a-b;当b<0时,a+b<a-b;当b=0岁,a+b=a-b.
点评 此题考查了代数式求值,弄清作差法比较大小是解本题的关键.

练习册系列答案
相关题目
12.已知二次函数y=x2-x+a(a>0),当自变量x取m时,其相应的函数值小于0,那么下列结论中正确的是( )
| A. | m-1>0 | B. | m-1<0 | ||
| C. | m-1=0 | D. | m-1与0的大小关系不确定 |
16. 如图是一块长为a,宽为b(a>b)的长方形空地,要将阴影部分绿化,则阴影面积是( )
如图是一块长为a,宽为b(a>b)的长方形空地,要将阴影部分绿化,则阴影面积是( )
 如图是一块长为a,宽为b(a>b)的长方形空地,要将阴影部分绿化,则阴影面积是( )
如图是一块长为a,宽为b(a>b)的长方形空地,要将阴影部分绿化,则阴影面积是( )| A. | a2b2 | B. | ab-πa2 | C. | $ab-\frac{π}{4}{b^2}$ | D. | $ab-\frac{π}{4}{a^2}$ |
17.将二次函数y=$\frac{1}{2}{x^2}$的图象向左移1个单位,再向下移2个单位后所得函数的关系式为( )
| A. | y=$\frac{1}{2}{({x+1})^2}$-2 | B. | y=$\frac{1}{2}{({x-1})^2}$-2 | C. | y=$\frac{1}{2}{({x+1})^2}$+2 | D. | y=$\frac{1}{2}{({x-1})^2}$+2 |
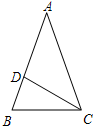 如图,在△ABC中,AB=AC,D为AB上一点,AD=CD,若∠ACD=40°,则∠B=70°.
如图,在△ABC中,AB=AC,D为AB上一点,AD=CD,若∠ACD=40°,则∠B=70°. 如图,G是边长为8的正方形ABCD的边BC上的一点,矩形DEFG的边EF过点A,GD=10.
如图,G是边长为8的正方形ABCD的边BC上的一点,矩形DEFG的边EF过点A,GD=10.