题目内容
18.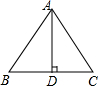 如图,在△ABC中,AB=AC=5cm,BC=6cm,AD平分∠BAC,则AD=4cm.
如图,在△ABC中,AB=AC=5cm,BC=6cm,AD平分∠BAC,则AD=4cm.
分析 根据等腰三角形的性质得到BD=$\frac{1}{2}$BC=3,AD⊥BC,根据勾股定理计算即可.
解答 解:∵AB=AC,AD平分∠BAC,
∴BD=$\frac{1}{2}$BC=3,AD⊥BC,
由勾股定理得,AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=4(cm),
故答案为:4.
点评 本题考查的是勾股定理,掌握直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2是解题的关键.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
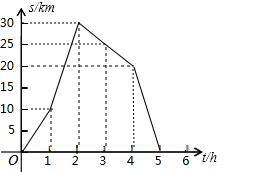 如图是小李骑自行车离家的距离s(km)与时间t(h)之间的关系.
如图是小李骑自行车离家的距离s(km)与时间t(h)之间的关系.