题目内容
8.(1)求值:已知y=$\sqrt{x-3}$+$\sqrt{3-x}$+8,求3x+2y的算术平方根;(2)化简求值(x$\sqrt{\frac{1}{x}}$+$\sqrt{4y}$)-($\sqrt{\frac{x}{4}}$-y$\sqrt{\frac{1}{y}}$),其中x=8,y=$\frac{1}{27}$.
分析 (1)根据二次根式的被开方数为非负数可得出x的值,进而得出y的值,代入代数式后求算术平方根即可;
(2)根据二次根式的性质及运算法则化简原式后将x、y的值代入计算可得.
解答 解:(1)根据题意得$\left\{\begin{array}{l}{x-3≥0}\\{3-x≥0}\end{array}\right.$,
解得:x=3,
当x=3时,y=8,
∴$\sqrt{3x+2y}$=$\sqrt{3×3+2×8}$=5;
(2)原式=$\sqrt{x}$+2$\sqrt{y}$-$\frac{\sqrt{x}}{2}$+$\sqrt{y}$
=$\frac{\sqrt{x}}{2}$+3$\sqrt{y}$,
当x=8,y=$\frac{1}{27}$时,
原式=$\frac{\sqrt{8}}{2}$+3×$\sqrt{\frac{1}{27}}$
=$\frac{2\sqrt{2}}{2}$+3×$\frac{1}{3\sqrt{3}}$
=$\sqrt{2}$+$\frac{\sqrt{3}}{3}$.
点评 本题主要考查二次根式的化简求值及二次根式有意义的条件,根据二次根式有意义条件得出x、y的值是根本,熟练掌握二次根式的性质及运算法则是解题的关键.

练习册系列答案
相关题目
17.已知△ABC中,BC=6,AC=3,CP⊥AB,垂足为P,则CP的长可能是( )
| A. | 2 | B. | 4 | C. | 5 | D. | 7 |
 已知抛物线y=x2-(k+2)x+$\frac{5k+2}{4}$和直线y=(k+1)x+(k+1)2.
已知抛物线y=x2-(k+2)x+$\frac{5k+2}{4}$和直线y=(k+1)x+(k+1)2.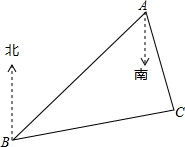 如图,B处在A处的南偏西45°方向,C处在A处的南偏东15°方向,C处在B处的北偏东80°方向,求∠ACB的度数.
如图,B处在A处的南偏西45°方向,C处在A处的南偏东15°方向,C处在B处的北偏东80°方向,求∠ACB的度数.
