题目内容
下列代数式:-x,2x2,-3x3,4x4,A,B,-19x19.
(1)所缺的代数式A是 ,B是 ;
(2)试写出第2014个和2015个代数式;
(3)试写出第n个和第(n+1)个代数式(n是正整数)
(1)所缺的代数式A是
(2)试写出第2014个和2015个代数式;
(3)试写出第n个和第(n+1)个代数式(n是正整数)
考点:单项式
专题:规律型
分析:(1)观察每个单项式的系数与x的指数,不看符号,都是从1开始的自然数,符号为奇数位置是正,偶数位置是负;
(2)利用(1)中规律进而得出第2 010个单项式和第2011个单项式.
(3)由(2)自然可推出第n项为(-1)n+1nxn,第(n+1)个单项式.
(2)利用(1)中规律进而得出第2 010个单项式和第2011个单项式.
(3)由(2)自然可推出第n项为(-1)n+1nxn,第(n+1)个单项式.
解答:解:(1)由-x,2x2,-3x3,4x4,…,19x19,-20x20可以得到:
每个单项式的系数的绝对值与x的指数相等;奇数项系数为负;偶数项系数为正.
∴单项式A是:-5x5,B是:6x6.
故答案为:-5x5,6x6;
(2)由第n项为(-1)nnxn可以得到第2014个单项式是2014x2014.第2015个单项式是-2015x2015;
(3)由第n项为(-1)nnxn可以得到:
第(n+1)个单项式是(-1)n+1(n+1)xn+1.
每个单项式的系数的绝对值与x的指数相等;奇数项系数为负;偶数项系数为正.
∴单项式A是:-5x5,B是:6x6.
故答案为:-5x5,6x6;
(2)由第n项为(-1)nnxn可以得到第2014个单项式是2014x2014.第2015个单项式是-2015x2015;
(3)由第n项为(-1)nnxn可以得到:
第(n+1)个单项式是(-1)n+1(n+1)xn+1.
点评:此题主要考查了数字规律,解答有关单项式的规律问题,要从系数、指数分析出数字规律,再去解决单项式.

练习册系列答案
相关题目
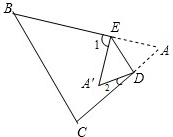 如图,把△ABC纸片沿DE折叠,点A落在四边形BCDE内部.
如图,把△ABC纸片沿DE折叠,点A落在四边形BCDE内部.