题目内容
已知△ABC的面积为18，有一边上的高为3，则三角形的周长最小值为 ．
考点：轴对称-最短路线问题
专题：
分析：根据题意画出图形，由面积为18，高为3，得到三角形此边长，作直线l与BC所在的直线平行，两平行线间的距离为3，作出B关于直线l的对称点B′，连接CB′，与直线l的交点为A，则AB+AC=AB′+AC=B′C，根据两点之间线段最短，此时△ABC的周长最小，在Rt△BCB′中，由BC及BB′的长，利用勾股定理求出CB′的长即为AB+AC的最小值，进而求出最小的周长．
解答：
解：根据题意画出图形，如图所示：
作出B关于直线l的对称点B′，连接CB′，与直线l交于点A，作AD⊥BC，
由BC=12，△ABC的面积为18，
根据
=18，
得到BC边长为12，
则BE=B′E=AD=3，BB′=6，
此时AB+AC=AB′+AC=B′C，△ABC的周长最小，
在直角三角形BCB′中，根据勾股定理得：B′C=
=
=6
，
则AB+AC=6
所以△ABC的最小周长为：6
+12．
故答案为：6
+12．
解：根据题意画出图形，如图所示：作出B关于直线l的对称点B′，连接CB′，与直线l交于点A，作AD⊥BC，
由BC=12，△ABC的面积为18，
根据
| 3AD |
| 2 |
得到BC边长为12，
则BE=B′E=AD=3，BB′=6，
此时AB+AC=AB′+AC=B′C，△ABC的周长最小，
在直角三角形BCB′中，根据勾股定理得：B′C=
| BB′2+BC2 |
| 62+122 |
| 5 |
则AB+AC=6
| 5 |
所以△ABC的最小周长为：6
| 5 |
故答案为：6
| 5 |
点评：此题考查了轴对称中最短路线的问题，涉及的知识有对称的性质，三角形的面积公式以及勾股定理，根据对称的性质确定出三角形周长最小时满足的图形，找出点B关于直线l的对称点B′，再根据两点之间线段最短得到B′C即为AB+AC的最小值是解本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
如图是由5个大小相同的正方体摆成的立体图形，它的正视图是（ ）A、 |
B、 |
C、 |
D、 |
如图所示，在Rt△ABC中，∠BAC=90°，∠B=30°，AC=1，线段AD是BC边上的中线，将△ADC沿直线BC平移，使点D与点C重合，得到△FCE，显然四边形ADEF是等腰梯形，再将△FCE绕点C顺时针旋转，设旋转角为α（0°＜α≤90°）．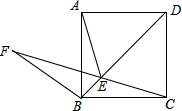
如图，在正方形ABCD的对角线上取点E，使得∠BAE=15°，连结AE，CE．延长CE到F，连结BF，使得BC=BF．若AB=1，则下列结论：
如图，在Rt△ABC中，∠C=90°，AC=3，点D为BC边上一点，且BD=2AD，∠ADC=60°，求AB的长．（结果保留根号）