题目内容
1.在Rt△ABC中,∠ACB=90°,M分别为AB和PE的中点,AD∥PC,且AD=PC(1)如图①,若CA=CB,请写出与线段DE相关的三个结论
(2)如图②,在Rt△ABC中,若∠CAB=30°,猜想DE与AC之间的数量关系和所在直线的位置关系,并说明理由
(3)如图③,改变点P的位置,且$\frac{BC}{AC}$=$\frac{5}{9}$,请你根据已知条件在图③中将图形补充完整,并直接写出DE与AC之间的数量关系和所在直线的位置关系,不必说明理由.

分析 (1)先连接AE,BP,BE,CD,构造平行四边形AEBP,平行四边形ADCP,进而得出四边形BCDE是平行四边形,即可得到DE∥BC,DE=BC,再根据CA=CB,∠ACB=90°,即可得出DE⊥AC,DE=AC;
(2)先连接AE,BP,BE,CD,构造平行四边形AEBP,平行四边形ADCP,进而得出四边形BCDE是平行四边形,即可得到DE∥BC,DE=BC,再根据Rt△ABC中,∠CAB=30°,∠ACB=90°,即可得到AC=$\sqrt{3}$BC,AC⊥BC,进而得出AC=$\sqrt{3}$DE,AC⊥DE;
(3)先连接AE,BP,BE,CD,构造平行四边形AEBP,平行四边形ADCP,进而得出四边形BCDE是平行四边形,即可得到DE∥BC,DE=BC,再根据Rt△ABC中,$\frac{BC}{AC}$=$\frac{5}{9}$,∠ACB=90°,即可得出BC=$\frac{5}{9}$AC,BC⊥AC,进而得到DE=$\frac{5}{9}$AC,DE⊥AC.
解答 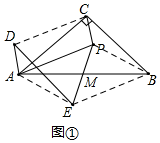 解:(1)DE∥BC,DE=BC,DE⊥AC,DE=AC.(答案不唯一)
解:(1)DE∥BC,DE=BC,DE⊥AC,DE=AC.(答案不唯一)
理由:如图,连接AE,BP,BE,CD,
∵M分别为AB和PE的中点,
∴四边形AEBP是平行四边形,
∴AP∥BE,AP=BE,
又∵AD∥PC,AD=PC,
∴四边形ADCP是平行四边形,
∴CD=AP,CD∥AP,
∴CD=BE,CD∥BE,
∴四边形BCDE是平行四边形,
∴DE∥BC,DE=BC,
又∵CA=CB,∠ACB=90°,
∴DE⊥AC,DE=AC;
(2)$\sqrt{3}$DE=AC,DE⊥AC.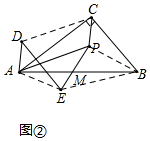
理由:如图,连接AE,BP,BE,CD,
∵M分别为AB和PE的中点,
∴四边形AEBP是平行四边形,
∴AP∥BE,AP=BE,
又∵AD∥PC,AD=PC,
∴四边形ADCP是平行四边形,
∴CD=AP,CD∥AP,
∴CD=BE,CD∥BE,
∴四边形BCDE是平行四边形,
∴DE∥BC,DE=BC,
又∵在Rt△ABC中,∠CAB=30°,∠ACB=90°,
∴AC=$\sqrt{3}$BC,AC⊥BC,
∴AC=$\sqrt{3}$DE,AC⊥DE;
(3)DE=$\frac{5}{9}$AC,DE⊥AC.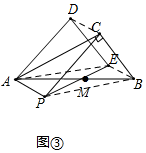
理由:如图,连接AE,BP,BE,CD,
∵M分别为AB和PE的中点,
∴四边形AEBP是平行四边形,
∴AP∥BE,AP=BE,
又∵AD∥PC,AD=PC,
∴四边形ADCP是平行四边形,
∴CD=AP,CD∥AP,
∴CD=BE,CD∥BE,
∴四边形BCDE是平行四边形,
∴DE∥BC,DE=BC,
又∵在Rt△ABC中,$\frac{BC}{AC}$=$\frac{5}{9}$,∠ACB=90°,
∴BC=$\frac{5}{9}$AC,BC⊥AC,
∴DE=$\frac{5}{9}$AC,DE⊥AC.
点评 本题属于相似形综合题,主要考查了平行四边形的判定与性质,等腰直角三角形的性质,含30°角的直角三角形的性质的综合应用,解决问题的关键是作辅助线构造平行四边形,依据平行四边形的对边平行且相等进行推导.解题时注意:在直角三角形中,30°角所对的直角边等于斜边的一半.

 字词句段篇系列答案
字词句段篇系列答案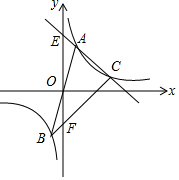 如图,已知直线y=3x与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,其中A(1,3),点C是反比例函数在第一象限的图象上不同于A的一点,直线AC交y轴于点E,直线BC交y轴于点F,则线段EF的长是( )
如图,已知直线y=3x与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,其中A(1,3),点C是反比例函数在第一象限的图象上不同于A的一点,直线AC交y轴于点E,直线BC交y轴于点F,则线段EF的长是( )| A. | 4 | B. | 5 | C. | 6 | D. | 变量 |
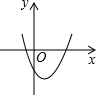 二次函数y=ax2+bx+c的图象如图所示,下列结论错误的是( )
二次函数y=ax2+bx+c的图象如图所示,下列结论错误的是( )| A. | a>0 | B. | b>0 | C. | c<0 | D. | ac<0 |
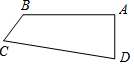 如图,四边形ABCD中,AB⊥AD于A,AB=8$\sqrt{6}$,AD=8$\sqrt{3}$,BC=7,CD=25,则四边形ABCD的面积为84+96$\sqrt{2}$.
如图,四边形ABCD中,AB⊥AD于A,AB=8$\sqrt{6}$,AD=8$\sqrt{3}$,BC=7,CD=25,则四边形ABCD的面积为84+96$\sqrt{2}$.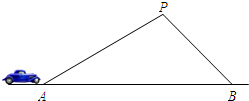 某条道路上通行车辆限速为60千米/时,在离道路50米的点P处建一个监测点,道路AB段为检测区(如图).在△ABP中,已知∠PAB=30°,∠PBA=45°,那么车辆通过AB段的时间在多少秒以内时,可认定为超速(精确到0.1秒)?(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,60千米/时=$\frac{50}{3}$米/秒)
某条道路上通行车辆限速为60千米/时,在离道路50米的点P处建一个监测点,道路AB段为检测区(如图).在△ABP中,已知∠PAB=30°,∠PBA=45°,那么车辆通过AB段的时间在多少秒以内时,可认定为超速(精确到0.1秒)?(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,60千米/时=$\frac{50}{3}$米/秒) 如图,以图中的A、B、C、D为端点的线段共有6条.
如图,以图中的A、B、C、D为端点的线段共有6条.