题目内容
14.对于一切正整数n,关于x的一元二次方程x2-(n+3)x-3n2=0的两个根记为an、bn,则$\frac{1}{{({a_1}-3)({b_1}-3)}}$+$\frac{1}{{({a_2}-3)({b_2}-3)}}$+…+$\frac{1}{{({a_9}-3)({b_9}-3)}}$=-$\frac{3}{10}$.分析 由根与系数的关系得an+bn=n+3,an•bn=-3n2,所以(an-3)(bn-3)=anbn-3(an+bn)+9=-3n2-3(n+3)+9=-3n(n+1),则$\frac{1}{({a}_{n}-3)({b}_{n}-3)}$=$\frac{1}{-3n(n+1)}$=-$\frac{1}{3}$($\frac{1}{n}$-$\frac{1}{n+1}$),然后代入即可求解.
解答 解:由根与系数的关系得an+bn=n+3,an•bn=-3n2,
所以(an-3)(bn-3)=anbn-3(an+bn)+9=-3n2-3(n+3)+9=-3n(n+1),
则$\frac{1}{({a}_{n}-3)({b}_{n}-3)}$=$\frac{1}{-3n(n+1)}$=-$\frac{1}{3}$($\frac{1}{n}$-$\frac{1}{n+1}$),
∴原式=-$\frac{1}{3}$(1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{9}$-$\frac{1}{10}$)
=-$\frac{1}{3}$×(1-$\frac{1}{10}$)
=-$\frac{1}{3}$×$\frac{9}{10}$
=-$\frac{3}{10}$,
故答案为:-$\frac{3}{10}$
点评 本题考查了根与系数的关系,关键是根据根与系数的关系求出一般形式再进行代入求值.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
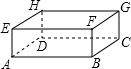 如图,长方体的长、宽、高分别为6cm,5cm,4cm,现有一只蜘蛛由A出发去捕食G处的昆虫,则这只蜘蛛的最短爬行路线的长为3$\sqrt{13}$cm.
如图,长方体的长、宽、高分别为6cm,5cm,4cm,现有一只蜘蛛由A出发去捕食G处的昆虫,则这只蜘蛛的最短爬行路线的长为3$\sqrt{13}$cm. 如图,在⊙O中,AB=AC,∠B=70°,则∠C=70°.
如图,在⊙O中,AB=AC,∠B=70°,则∠C=70°.