题目内容
16．分式方程$\frac{x}{x-2}$-$\frac{2}{{x}^{2}-4}$=1的解是x=-1．分析 方程两边都乘以（x+2）（x-2）得到x（x+2）-2=（x+2）（x-2），解得x=-1，然后进行检验确定分式方程的解．
解答 解：$\frac{x}{x-2}$-$\frac{2}{{x}^{2}-4}$=1，
去分母得x（x+2）-2=（x+2）（x-2），
解得x=-1，
检验：当x=-1时，（x+2）（x-2）≠0，
所以原方程的解为x=-1．
故答案为：x=-1．
点评 本题考查了解分式方程：先去分母，把分式方程转化为整式方程，再解整式方程，然后把整式方程的解代入分式方程进行检验，最后确定分式方程的解．
练习册系列答案
相关题目
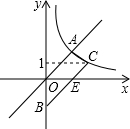如图，梯形AOBC的顶点A，C在反比例函数图象上，OA∥BC，上底边OA在直线y=x上，下底边BC交y轴于B（0，-4），则四边形AOBC的面积为2$\sqrt{5}$+10．
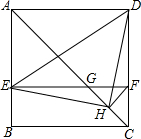如图，在正方形ABCD中，AC为对角线，E为AB上一点，过点E作EF∥AD，与AC、DC分别交于点G、F，H为CG的中点，连接DE、EH、DH、FH．下列结论：①EG=DF；②∠AEH+∠ADH=180°；③△EHF≌△DHC；④若$\frac{AE}{AB}$=$\frac{1}{3}$，则3S△EDH=13S△DHC，其中结论正确的有①②③（填写序号）．
如图，一次函数y=kx+5（k为常数，且k≠0）的图象与反比例函数y=-$\frac{8}{x}$的图象有一交点为A（-2，b）点．