题目内容
5.化简:$\frac{1}{{a}^{2}-a}$+$\frac{a-3}{{a}^{2}-1}$.分析 根据分式的性质,可化成同分母的分式加减,根据同分母分式的加减,可得答案.
解答 解:原式=$\frac{a+1}{a(a-1)(a+1)}$+$\frac{a(a-3)}{a(a+1)(a-1)}$=$\frac{{a}^{2}-2a+1}{{a}^{3}-a}$.
点评 本题考查了分式的加减,利用分式的性质化成同分母分式是解题关键.

练习册系列答案
相关题目
17.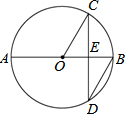 如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为6,则圆心O到弦CD的距离OE长为( )
如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为6,则圆心O到弦CD的距离OE长为( )
 如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为6,则圆心O到弦CD的距离OE长为( )
如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为6,则圆心O到弦CD的距离OE长为( )| A. | 6 | B. | 5 | C. | 3$\sqrt{3}$ | D. | 3 |
14.把抛物线y=-x2向右平移1个单位,然后向上平移3个单位,则平移后抛物线的解析式为( )
| A. | y=-(x-1)2-3 | B. | y=-(x+1)2-3 | C. | y=-(x-1)2+3 | D. | y=-(x+1)2+3 |
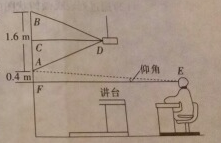 教室的屏幕AB、投影仪D及教室中间前排学生位置左视图如图所示,为了确保眼睛不易疲劳,安装时要求教室中间前排学生与屏幕的距离≥屏幕高度的2倍.现测得屏幕的高度AB=1.6m,在屏幕的正中央C的前方放的投影仪离屏幕的距离CD=2m,前排学生的眼睛E看屏幕底端A的仰角∠AEF=6°,屏幕底端A到水平线EF的距离AF=0.4m.
教室的屏幕AB、投影仪D及教室中间前排学生位置左视图如图所示,为了确保眼睛不易疲劳,安装时要求教室中间前排学生与屏幕的距离≥屏幕高度的2倍.现测得屏幕的高度AB=1.6m,在屏幕的正中央C的前方放的投影仪离屏幕的距离CD=2m,前排学生的眼睛E看屏幕底端A的仰角∠AEF=6°,屏幕底端A到水平线EF的距离AF=0.4m.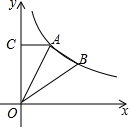 如图,O为坐标原点,A、B是函数y=$\frac{9\sqrt{2}}{x}$(x>0)的图象上的两点,过A作AC⊥y轴于C,若AB⊥OA,且△OAB与△ACO相似,则点B的坐标为(6,$\frac{3\sqrt{2}}{2}$).
如图,O为坐标原点,A、B是函数y=$\frac{9\sqrt{2}}{x}$(x>0)的图象上的两点,过A作AC⊥y轴于C,若AB⊥OA,且△OAB与△ACO相似,则点B的坐标为(6,$\frac{3\sqrt{2}}{2}$).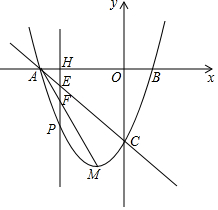 在平面直角坐标系中,已知抛物线y=x2+bx+c的顶点M的坐标为(-1,-4),且与x轴交于点A,点B(点A在点B的左边),与y轴交于点C.
在平面直角坐标系中,已知抛物线y=x2+bx+c的顶点M的坐标为(-1,-4),且与x轴交于点A,点B(点A在点B的左边),与y轴交于点C.
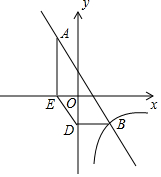 已知:如图,一次函数y=-2x+1与反比例函数y=$\frac{k}{x}$的图象有两个交点A(-1,m)和B,过点A作AE⊥x轴,垂足为点E;过点B作BD⊥y轴,垂足为点D,且点D的坐标为(0,-2),连接DE.
已知:如图,一次函数y=-2x+1与反比例函数y=$\frac{k}{x}$的图象有两个交点A(-1,m)和B,过点A作AE⊥x轴,垂足为点E;过点B作BD⊥y轴,垂足为点D,且点D的坐标为(0,-2),连接DE.