题目内容
6. 如图,一次函数y=kx+5(k为常数,且k≠0)的图象与反比例函数y=-$\frac{8}{x}$的图象有一交点为A(-2,b)点.
如图,一次函数y=kx+5(k为常数,且k≠0)的图象与反比例函数y=-$\frac{8}{x}$的图象有一交点为A(-2,b)点.(1)求一次函数的表达式;
(2)若将直线AB向下平移m(m>0)个单位长度后与反比例函数的图象有且只有一个公共点,求m的值.
分析 (1)先利用反比例函数解析式求出b,得到A点坐标为(-2,4),然后把A点坐标代入y=kx+5中求出k,从而得到一次函数解析式;
(2)由于将直线AB向下平移m(m>0)个单位长度得直线解析式为y=kx+5-m,则直线y=kx+5-m与反比例函数有且只有一个公共点,即方程组,只有一组解,然后消去y得到关于x的二次函数,再根据判别式的意义得到关于m的方程,最后解方程求出m的值.
解答 解:(1)把A(-2,b)代入y=-$\frac{8}{x}$得b=-$\frac{8}{-2}$=4,
所以A点坐标为(-2,4),
把A(-2,4)代入y=kx+5得-2k+5=4,解得k=$\frac{1}{2}$,
所以一次函数解析式为y=$\frac{1}{2}$x+5;
(2)令直线AB向下平移m个单位得到的解析式为y=$\frac{1}{2}$x+5-m
由$\left\{\begin{array}{l}{y=-\frac{8}{x}}\\{y=\frac{1}{2}x+5-m}\end{array}\right.$得消去y得-$\frac{8}{x}$=$\frac{1}{2}$x+5-m,
整理得$\frac{1}{2}$x2-(m-5)x+8=0,
∵图象只有一个公共点,
∴△=(m-5)2-4×$\frac{1}{2}$×8=0,解得m=9或m=1.
点评 本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.也考查了一次函数与几何变换.

练习册系列答案
相关题目
17.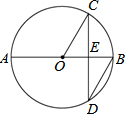 如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为6,则圆心O到弦CD的距离OE长为( )
如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为6,则圆心O到弦CD的距离OE长为( )
 如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为6,则圆心O到弦CD的距离OE长为( )
如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为6,则圆心O到弦CD的距离OE长为( )| A. | 6 | B. | 5 | C. | 3$\sqrt{3}$ | D. | 3 |
14.把抛物线y=-x2向右平移1个单位,然后向上平移3个单位,则平移后抛物线的解析式为( )
| A. | y=-(x-1)2-3 | B. | y=-(x+1)2-3 | C. | y=-(x-1)2+3 | D. | y=-(x+1)2+3 |
1.一个多边形除了一个内角外,其余各内角之和为2570°,则这个内角的度数为( )
| A. | 120° | B. | 130° | C. | 135° | D. | 150° |
18.下列各式由左到右的变形中,属于分解因式的是( )
| A. | a(m+n)=am+an | B. | a2-b2-c2=(a-b)(a+b)-c2 | ||
| C. | 10x2-5x=5x(2x-1) | D. | x2-16+6x=(x+4)(x-4)+6x |
 如图,在△ABC中,D、E分别是边AB、AC的中点,则△ADE与△ABC的面积比S△ADE:S△ABC=1:4.
如图,在△ABC中,D、E分别是边AB、AC的中点,则△ADE与△ABC的面积比S△ADE:S△ABC=1:4.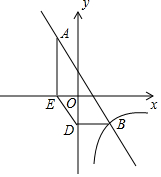 已知:如图,一次函数y=-2x+1与反比例函数y=$\frac{k}{x}$的图象有两个交点A(-1,m)和B,过点A作AE⊥x轴,垂足为点E;过点B作BD⊥y轴,垂足为点D,且点D的坐标为(0,-2),连接DE.
已知:如图,一次函数y=-2x+1与反比例函数y=$\frac{k}{x}$的图象有两个交点A(-1,m)和B,过点A作AE⊥x轴,垂足为点E;过点B作BD⊥y轴,垂足为点D,且点D的坐标为(0,-2),连接DE.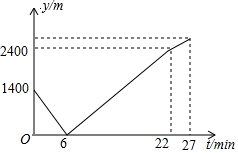 小东家与学校之间是一条笔直的公路,早饭后,小东步行前往学校,途中发现忘带画板,停下给妈妈打电话,妈妈接到电话后,带上画板马上赶往学校,同时小东沿原路返回,两人相遇后,小东立即赶往学校,妈妈沿原路返回16min到家,再过5min小东到达学校,小东始终以100m/min的速度步行,小东和妈妈的距离y(单位:m)与小东打完电话后的步行时间t(单位:min)之间的函数关系如图所示,下列四种说法:
小东家与学校之间是一条笔直的公路,早饭后,小东步行前往学校,途中发现忘带画板,停下给妈妈打电话,妈妈接到电话后,带上画板马上赶往学校,同时小东沿原路返回,两人相遇后,小东立即赶往学校,妈妈沿原路返回16min到家,再过5min小东到达学校,小东始终以100m/min的速度步行,小东和妈妈的距离y(单位:m)与小东打完电话后的步行时间t(单位:min)之间的函数关系如图所示,下列四种说法: