题目内容
14.商店只有雪碧、可乐、果汁、奶汁四种饮料,每种饮料数量充足,某同学去该店购买饮料,每种饮料被选中的可能性相同.(1)若他去买一瓶饮料,则他买到奶汁的概率是$\frac{1}{4}$;
(2)若他两次去买饮料,每次买一瓶,且两次所买饮料品种不同,请用树状图或列表法求出他恰好买到雪碧和奶油的概率.
分析 (1)由商店只有雪碧、可乐、果汁、奶汁四种饮料,每种饮料数量充足,某同学去该店购买饮料,每种饮料被选中的可能性相同,直接利用概率公式求解即可求得答案;
(2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与他恰好买到雪碧和奶汁的情况,再利用概率公式即可求得答案.
解答 解:
解:(1)∵商店只有雪碧、可乐、果汁、奶汁四种饮料,每种饮料数量充足,某同学去该店购买饮料,每种饮料被选中的可能性相同,
∴他去买一瓶饮料,则他买到奶汁的概率是:$\frac{1}{4}$;
故答案为:$\frac{1}{4}$;
(2)画树状图得:
∵共有12种等可能的结果,他恰好买到雪碧和奶汁的有2种情况,
∴他恰好买到雪碧和奶汁的概率为:$\frac{2}{12}$=$\frac{1}{6}$.
点评 本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
9.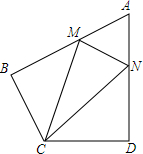 如图,在四边形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,点M,N分别在AB,AD边上,若AM:MB=AN:ND=1:2,则sin∠MCN=( )
如图,在四边形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,点M,N分别在AB,AD边上,若AM:MB=AN:ND=1:2,则sin∠MCN=( )
 如图,在四边形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,点M,N分别在AB,AD边上,若AM:MB=AN:ND=1:2,则sin∠MCN=( )
如图,在四边形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,点M,N分别在AB,AD边上,若AM:MB=AN:ND=1:2,则sin∠MCN=( )| A. | $\frac{3\sqrt{3}}{13}$ | B. | $\frac{3\sqrt{3}}{14}$ | C. | $\frac{\sqrt{3}}{5}$ | D. | $\sqrt{5}$-2 |
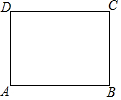 在矩形ABCD中,AB=4,BC=3,点P在边AB上.若将△DAP沿DP折叠,使点A落在矩形ABCD的对角线上,则AP的长为$\frac{3}{2}$或$\frac{9}{4}$.
在矩形ABCD中,AB=4,BC=3,点P在边AB上.若将△DAP沿DP折叠,使点A落在矩形ABCD的对角线上,则AP的长为$\frac{3}{2}$或$\frac{9}{4}$.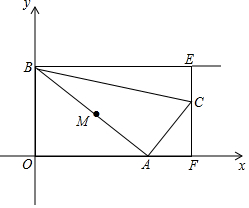 如图,点A从坐标原点出发,沿x轴的正方向运动,点B坐标为(0,4),M是线段AB的中点,将点M绕点A顺时针方向旋转90°得到点C,过点C作x轴的垂线,垂足为F,过点B作y轴的垂线与直线CF相交于点E,连接AC,BC,设点A的横坐标为t.
如图,点A从坐标原点出发,沿x轴的正方向运动,点B坐标为(0,4),M是线段AB的中点,将点M绕点A顺时针方向旋转90°得到点C,过点C作x轴的垂线,垂足为F,过点B作y轴的垂线与直线CF相交于点E,连接AC,BC,设点A的横坐标为t.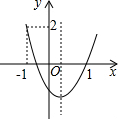 如图,二次函数y=ax2+bx+c的图象开口向上,图象经过点(-1,2)和点(1,0),且与y轴交于负半轴,给出下面四个结论:
如图,二次函数y=ax2+bx+c的图象开口向上,图象经过点(-1,2)和点(1,0),且与y轴交于负半轴,给出下面四个结论: