题目内容
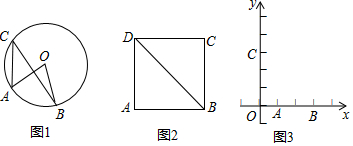
5. 在矩形ABCD中,AB=4,BC=3,点P在边AB上.若将△DAP沿DP折叠,使点A落在矩形ABCD的对角线上,则AP的长为$\frac{3}{2}$或$\frac{9}{4}$.
在矩形ABCD中,AB=4,BC=3,点P在边AB上.若将△DAP沿DP折叠,使点A落在矩形ABCD的对角线上,则AP的长为$\frac{3}{2}$或$\frac{9}{4}$.
分析 分两种情况探讨:点A落在矩形对角线BD上,点A落在矩形对角线AC上,在直角三角形中利用勾股定理列出方程,通过解方程可得答案.
解答 解:①点A落在矩形对角线BD上,如图1,
∵AB=4,BC=3,
∴BD=5,
根据折叠的性质,AD=A′D=3,AP=A′P,∠A=∠PA′D=90°,
∴BA′=2,
设AP=x,则BP=4-x,
∵BP2=BA′2+PA′2,
∴(4-x)2=x2+22,
解得:x=$\frac{3}{2}$,
∴AP=$\frac{3}{2}$;
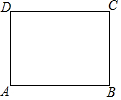
②点A落在矩形对角线AC上,如图2,
根据折叠的性质可知DP⊥AC,
∴△DAP∽△ABC,
∴$\frac{AD}{AP}$=$\frac{AB}{BC}$,
∴AP=$\frac{AD•BC}{AB}$=$\frac{9}{4}$.
故答案为:$\frac{3}{2}$或$\frac{9}{4}$.
点评 本题考查了折叠问题、勾股定理,矩形的性质以及三角形相似的判定与性质;解题中,找准相等的量是正确解答题目的关键.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案
相关题目
 如图所示,函数y1=|x|和y2=kx+b的图象相交于(-1,1),(2,2)两点.当y1>y2时,x的取值范围是x>2或x<-1.
如图所示,函数y1=|x|和y2=kx+b的图象相交于(-1,1),(2,2)两点.当y1>y2时,x的取值范围是x>2或x<-1.